3 maneres de calcular la pressió de vapor

2024 Autora: Jason Gerald | [email protected]. Última modificació: 2024-02-01 14:12

Alguna vegada heu deixat unes ampolles d’aigua al sol calent durant unes hores i heu sentit un petit xiulet quan l’obrí? Això es deu a un principi anomenat pressió de vapor. En química, la pressió de vapor és la pressió que exerceixen les parets d’un recipient tancat quan la substància química que s’hi evapora (es converteix en gas). Per trobar la pressió de vapor a una temperatura determinada, utilitzeu l'equació de Clausius-Clapeyron: ln (P1 / P2) = (ΔH_vapor/ R) ((1 / T2) - (1 / T1)).

Pas

Mètode 1 de 3: utilitzar l'equació de Clausius-Clapeyron

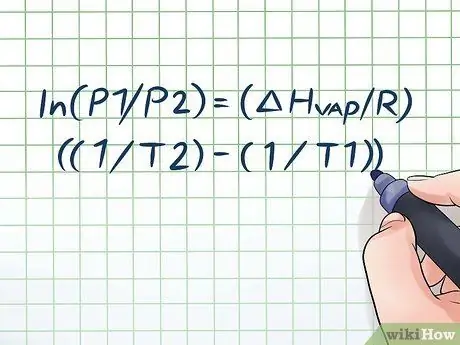
Pas 1. Escriviu l’equació de Clausius-Clapeyron

La fórmula que s’utilitza per calcular la pressió de vapor amb el canvi de la pressió de vapor al llarg del temps s’anomena equació de Clausius – Clapeyron (que porta el nom dels físics Rudolf Clausius i Benoît Paul mile Clapeyron.) Aquesta és bàsicament la fórmula que necessitareu per resoldre la majoria de tipus de problemes. Les preguntes sobre la pressió de vapor es troben sovint a les classes de física i química. La fórmula és així: ln (P1 / P2) = (ΔH_vapor/ R) ((1 / T2) - (1 / T1)). En aquesta fórmula, les variables representen:

• H_vapor:

  L’entalpia de vaporització d’un líquid. Aquesta entalpia normalment es pot trobar a la taula de la part posterior del llibre de text de química.

• R:

  La constant de gas real / universal, o 8,314 J / (K × Mol).

• P1:

  La temperatura a la qual es coneix la pressió de vapor (o temperatura inicial).

• T2:

  La temperatura a la qual es desconeix / es volia trobar la pressió de vapor (o la temperatura final).

• P1 i P2:

  Pressió de vapor a les temperatures T1 i T2, respectivament.

Pas 2. Introduïu les variables que coneixeu

L’equació de Clausius-Clapeyron sembla complicada perquè té moltes variables diferents, però en realitat no és tan difícil si es disposa de la informació adequada. La majoria de problemes bàsics de pressió de vapor enumeraran dos valors de temperatura i un valor de pressió o dos valors de pressió i un valor de temperatura; un cop ho comproveu, resoldre aquesta equació és molt fàcil.

• Per exemple, diguem que se'ns diu que tenim un recipient ple de líquid a 295 K la pressió de vapor és d'1 atmosfera (atm). La nostra pregunta és: Quina és la pressió de vapor a 393 K? Tenim dos valors de temperatura i un de pressió, de manera que podem trobar els altres valors de pressió mitjançant l’equació de Clausius-Clapeyron. En connectar les nostres variables, ho aconseguim ln (1 / P2) = (ΔH_vapor/ R) ((1/393) - (1/295)).
• Tingueu en compte que, per a l’equació de Clausius-Clapeyron, sempre heu d’utilitzar el valor de temperatura Kelvin. Podeu utilitzar qualsevol valor de pressió sempre que els valors de P1 i P2 siguin els mateixos.

Pas 3. Introduïu les constants

L’equació de Clausius-Clapeyron té dues constants: R i H_vapor. R sempre és igual a 8,314 J / (K × Mol). Tanmateix, H_vapor (entalpia de vaporització) depèn de la substància la pressió de vapor que busqueu. Com s’ha indicat anteriorment, normalment podeu trobar els valors de H_vapor per a diverses substàncies a la part posterior d'un llibre de text de química o física o en línia (com, per exemple, aquí).

• En el nostre exemple, suposem que el nostre líquid és aigua pura.

  Si mirem a la taula els valors de H_vapor, trobem que H_vapor l’aigua pura té uns 40,65 KJ / mol. Com que el nostre valor H està en joules i no en kilojoules, el podem convertir a 40.650 J / mol.

• Connectant les nostres constants, ho aconseguim ln (1 / P2) = (40.650 / 8, 314) ((1/393) - (1/295)).

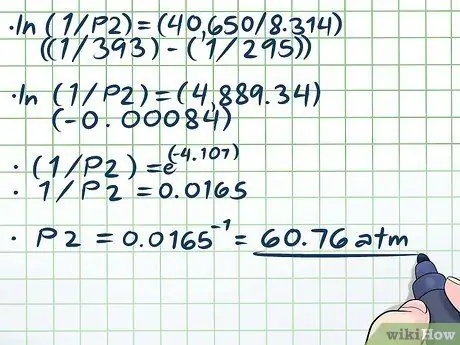
Pas 4. Resol l’equació

Un cop incloses totes les variables a l'equació, excepte la que busqueu, procediu a resoldre l'equació segons les regles de l'àlgebra ordinària.

• L’única part difícil de resoldre la nostra equació (ln (1 / P2) = (40.650 / 8, 314) ((1/393) - (1/295))) està resolent el registre natural (ln). Per eliminar el registre natural, només cal utilitzar els dos costats de l’equació com a exponents de la constant matemàtica e. En altres paraules, ln (x) = 2 → e^{ln (x)} = e² → x = e².

• Ara resolem la nostra equació:
• ln (1 / P2) = (40.650 / 8, 314) ((1/393) - (1/295))
• ln (1 / P2) = (4889, 34) (- 0, 00084)
• (1 / P2) = e^{(-4, 107)}
• 1 / P2 = 0,0165

• P2 = 0,0165^-1 = 60, 76 atm.

  Això té sentit: en un recipient tancat, augmentar la temperatura fins a gairebé 100 graus (fins a gairebé 20 graus per sobre del punt d’ebullició) produirà molt vapor, augmentant la pressió ràpidament.

Mètode 2 de 3: Trobar la pressió de vapor amb solució dissolta

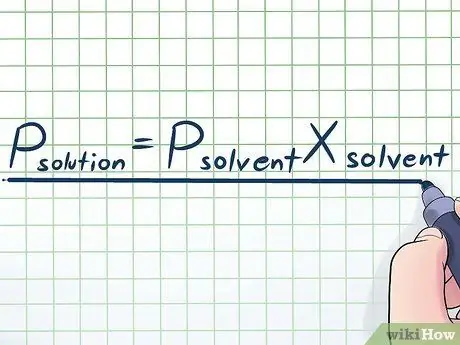
Pas 1. Escriviu la llei de Raoult

A la vida real, poques vegades treballem amb un líquid pur; normalment, treballem amb un líquid que és una barreja de diverses substàncies diferents. Algunes de les mescles més utilitzades es fan dissolent una petita quantitat d'un determinat producte químic anomenat solut en molts productes químics anomenats dissolvent per obtenir una solució. En aquests casos, és útil conèixer una equació anomenada Llei de Raoult (que porta el nom del físic François-Marie Raoult), que s’escriu així: Pàg_solut= P_solventX_solvent. En aquesta fórmula, les variables representen;

• Pàg_solut:

  Pressió de vapor de tota la solució (tots els elements combinats)

• Pàg_solvent:

  Pressió de vapor del dissolvent

• X_solvent:

  Fracció molar de dissolvent

• No us preocupeu si no coneixeu termes com a fracció molar: els explicarem en els propers passos.

Pas 2. Determineu el dissolvent i el solut de la solució

Abans de poder calcular la pressió de vapor d’un líquid barrejat, heu d’identificar les substàncies que utilitzeu. Com a recordatori, es forma una solució quan un solut es dissol en un dissolvent: el producte químic que es dissol sempre s’anomena solut i el producte químic que el fa dissoldre sempre s’anomena dissolvent.

• Treballem amb els exemples senzills d’aquesta secció per il·lustrar els conceptes que comentem. Per al nostre exemple, suposem que volem trobar la pressió de vapor de l'almívar de sucre. Tradicionalment, el xarop de sucre és sucre soluble en aigua (proporció 1: 1), de manera que podem dir-ho el sucre és el nostre solut i l’aigua el nostre dissolvent.
• Tingueu en compte que la fórmula química de la sacarosa (sucre de taula) és C₁₂H₂₂O₁₁. Aquesta fórmula química serà molt important.

Pas 3. Cerqueu la temperatura de la solució

Com hem vist a la secció anterior de Clausius Clapeyron, la temperatura d’un líquid afectarà la seva pressió de vapor. En general, com més alta sigui la temperatura, més gran serà la pressió de vapor; a mesura que augmenti la temperatura, més líquid s’evapora i forma vapor, augmentant la pressió al contenidor.

En el nostre exemple, diguem que la temperatura del xarop de sucre en aquest moment és 298 K (uns 25 C).

Pas 4. Trobeu la pressió de vapor del dissolvent

Els materials químics de referència solen tenir valors de pressió de vapor per a moltes substàncies i compostos d’ús habitual, però aquests valors de pressió solen ser vàlids només si la substància té una temperatura de 25 C / 298 K o el seu punt d’ebullició. Si la vostra solució té una d’aquestes temperatures, podeu utilitzar un valor de referència, però si no, haureu de trobar la pressió de vapor a aquesta temperatura.

• El Clausius-Clapeyron us pot ajudar: utilitzeu una pressió de vapor de referència i 298 K (25 C) per a P1 i T1 respectivament.
• En el nostre exemple, la nostra barreja té una temperatura de 25 C, de manera que podem utilitzar fàcilment la nostra fàcil taula de referència. Sabem que a 25 C, l’aigua té una pressió de vapor de 23,8 mm HG

Pas 5. Cerqueu la fracció molar del vostre dissolvent

L’últim que hem de fer abans de solucionar-ho és trobar la fracció molar del nostre dissolvent. Trobar la fracció molar és fàcil: només cal convertir els compostos en mols i, a continuació, trobar el percentatge de cada compost en el nombre total de mols de la substància. En altres paraules, la fracció mol de cada compost és igual a (mols de compost) / (nombre total de mols en la substància).

• Suposem que la nostra recepta per a ús de xarop de sucre 1 litre d’aigua i 1 litre de sacarosa (sucre).

  En aquest cas, hem de trobar el nombre de mols de cada compost. Per fer-ho, trobarem la massa de cada compost i, a continuació, utilitzarem la massa molar de la substància per convertir-la en mols.

• Massa (1 L d’aigua): 1.000 grams (g)
• Massa (1 L de sucre cru): aproximadament 1.056, 8 g
• Moles (aigua): 1.000 grams × 1 mol / 18.015 g = 55.51 mol
• Moles (sacarosa): 1.056, 7 grams × 1 mol / 342.2965 g = 3.08 mols (tingueu en compte que podeu trobar la massa molar de la sacarosa a partir de la seva fórmula química, C₁₂H₂₂O₁₁.)
• Moles totals: 55,51 + 3,08 = 58,59 mol
• Fracció molar d’aigua: 55, 51/58, 59 = 0, 947

Pas 6. Acabeu

Finalment, tenim tot el necessari per resoldre la nostra equació de la llei de Raoult. Aquesta part és molt senzilla: només cal que connecteu els valors de les variables de l’equació simplificada de la Llei de Raoult al principi d’aquesta secció (Pàg_solut = P_solventX_solvent).

• Introduint els nostres valors, obtenim:
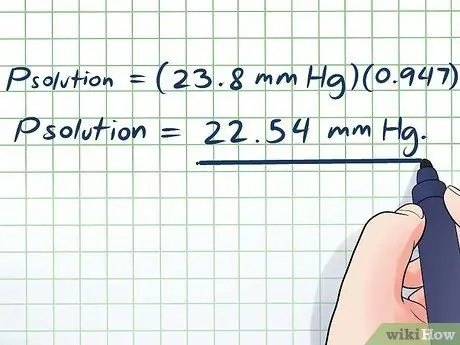
• Pàg_solució = (23,8 mm Hg) (0, 947)

• Pàg_solució = 22,54 mm Hg.

  El resultat té sentit: en termes de mol, hi ha molt poc sucre dissolt en molta aigua (tot i que en termes del món real, tots dos ingredients tenen el mateix volum), de manera que la pressió de vapor només disminuirà lleugerament.

Mètode 3 de 3: trobar la pressió de vapor en casos especials

Pas 1. Aneu amb compte amb les condicions estàndard de temperatura i pressió

Els científics solen utilitzar un conjunt de valors de temperatura i pressió com a "estàndard" fàcil d'utilitzar. Aquests valors s’anomenen temperatura i pressió estàndard (o STP). Els problemes de pressió de vapor solen referir-se a les condicions STP, per la qual cosa és important recordar aquests valors. Els valors STP es defineixen com:

• Temperatura: 273, 15 K / 0 C / 32 F.
• Pressió: 760 mm Hg / 1 ca / 101, 325 kilopascals

Pas 2. Reordeneu l’equació de Clausius-Clapeyron per trobar les altres variables

En el nostre exemple de la primera part, vam veure que l’equació de Clausius – Clapeyron és molt útil per trobar la pressió de vapor de substàncies pures. Tot i això, no totes les preguntes us demanaran que busqueu P1 o P2; molts us demanaran que trobeu el valor de la temperatura o, de vegades, fins i tot el valor H._vapor. Afortunadament, en aquests casos, encertar la resposta és simplement reordenar l’equació de manera que les variables que voleu resoldre estiguin separades per un costat del signe igual.

• Per exemple, diguem que tenim un líquid desconegut amb una pressió de vapor de 25 torr a 273 K i 150 torr a 325 K i volem trobar l’entalpia de vaporització d’aquest líquid (ΔH_vapor). Ho podem resoldre així:
• ln (P1 / P2) = (ΔH_vapor/ R) ((1 / T2) - (1 / T1))
• (ln (P1 / P2)) / ((1 / T2) - (1 / T1)) = (ΔH_vapor/ R)
• R × (ln (P1 / P2)) / ((1 / T2) - (1 / T1)) = H_vapor Ara introduïm els nostres valors:
• 8, 314 J / (K × Mol) × (-1, 79) / (- 0, 00059) = H_vapor
• 8, 314 J / (K × Mol) × 3.033, 90 = H_vapor = 25.223, 83 J / mol

Pas 3. Calculeu la pressió de vapor del solut quan la substància produeix vapor

En el nostre exemple de la Llei Raoult anterior, el nostre solut, el sucre, no exerceix cap pressió a si mateix a temperatures normals (penseu: quan va ser l'última vegada que vau veure evaporar un bol de sucre al vostre armari superior?). s'evapori, això afectarà la pressió de vapor. Ho expliquem mitjançant una versió modificada de l’equació de la llei de Raoult: Pàg_solució = (P_compostX_compost) El símbol sigma (Σ) significa que només necessitem sumar totes les pressions de vapor dels diferents compostos per obtenir la nostra resposta.

• Per exemple, diguem que tenim una solució formada per dos productes químics: benzè i tolueno. El volum total de la solució és de 12 mil·lilitres (mL); 60 mL de benzè i 60 mL de toluene. La temperatura de la solució és de 25 ° C i la pressió de vapor de cadascun d’aquests productes químics a 25 ° C és de 95,1 mm Hg per al benzè i 28,4 mm Hg per al tolueno. Amb aquests valors, trobeu la pressió de vapor de la solució. Ho podem fer de la següent manera, fent servir valors de densitat estàndard, massa molar i pressió de vapor per als nostres dos productes químics:
• Massa (benzè): 60 mL = 0,060 L i vegades 876,50 kg / 1.000 L = 0,053 kg = 53 g
• Massa (toluen): 0,060 L i vegades 866, 90 kg / 1.000 L = 0,052 kg = 52 g
• Mol (benzè): 53 g × 1 mol / 78, 11 g = 0,679 mol
• Moles (toluene): 52 g × 1 mol / 92, 14 g = 0,564 mol
• Moles totals: 0,679 + 0,564 = 1,243
• Fracció molar (benzè): 0,679 / 1, 243 = 0,546
• Fracció molar (toluene): 0,564 / 1, 243 = 0,454
• Solució: P_solució = P_benzèX_benzè + P_toluèX_toluè
• Pàg_solució = (95,1 mm Hg) (0, 546) + (28,4 mm Hg) (0, 454)
• Pàg_solució = 51,92 mm Hg + 12,89 mm Hg = 64, 81 mm Hg

Consells

• Per utilitzar l’equació de Clausius Clapeyron anterior, s’ha de mesurar la temperatura en Kelvin (escrita com a K). Si teniu la temperatura en centígrads, heu de convertir-la mitjançant la fórmula següent: T_k = 273 + T_c
• Es poden utilitzar els mètodes anteriors perquè l'energia és exactament proporcional a la quantitat de calor aplicada. La temperatura del líquid és l’únic factor ambiental que afecta la pressió de vapor.