- Autora Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-16 19:15.
- Última modificació 2025-01-23 12:10.
La velocitat és un càlcul de la velocitat amb què es mou alguna cosa alhora. Si alguna vegada heu mirat el velocímetre d’un cotxe en moviment, veureu el recompte de velocitat: com més lluny viatgi l’agulla, més gran serà la velocitat del vehicle. Hi ha diverses maneres de calcular la velocitat, en funció del tipus d'informació que tingueu. En general, la fórmula velocitat = distància / temps (o k = j / w) és la forma més senzilla de calcular la velocitat.
Pas
Mètode 1 de 3: utilitzar fórmules de càlcul de velocitat estàndard

Pas 1. Cerqueu la distància que ha recorregut un objecte
La fórmula bàsica que utilitza la majoria de la gent per trobar la velocitat d’alguna cosa és molt fàcil d’utilitzar. En primer lloc, cal saber "quanta distància ha recorregut l'objecte mesurat". En altres paraules, quina distància hi ha entre el punt inicial i el punt final de l'objecte?
Aquesta fórmula és més fàcil d’entendre mitjançant un exemple. Diguem que viatgem en cotxe fins a un parc infantil durant "161 quilòmetres". En uns quants passos, podem utilitzar aquesta informació per completar el càlcul de la fórmula

Pas 2. Cerqueu el temps que triga l'objecte a recórrer aquesta distància
La següent informació que necessiteu és quant de temps triga l’objecte a arribar a una distància determinada. En altres paraules, quant de temps triga l'objecte a moure's del punt d'inici al punt final?
En aquest exemple, suposem que l'objecte dura aprox. dues hores per arribar a la destinació.

Pas 3. Divideix la distància pel temps que es triga a trobar la velocitat de l'objecte
Només necessiteu aquestes dues informacions per conèixer la velocitat de l'objecte. La distància al temps és igual a la velocitat de l'objecte.
En aquest exemple, 161 quilòmetres / 2 hores = 80,5 quilòmetres / hora.

Pas 4. No oblideu la unitat utilitzada
És molt important utilitzar les unitats correctes a la resposta (com ara quilòmetres per hora, etc.) Sense aquestes unitats, és molt difícil per a la gent entendre el significat de la vostra resposta. També podeu perdre punts si utilitzeu la unitat equivocada quan feu tasques des de l’escola.
La unitat de velocitat és unitat de distància a unitat de temps. Per exemple, com que mesurem la distància en quilòmetres i el temps en hores, les unitats utilitzades són quilòmetres / hora (o quilòmetres per hora).
Mètode 2 de 3: resolució de càlculs més difícils

Pas 1. Cerqueu diverses variables diferents per resoldre el problema de la distància i el temps
Un cop hàgiu entès la fórmula bàsica per a la velocitat, podeu utilitzar-la per fer càlculs diferents de la velocitat. Per exemple, si al principi només coneixeu la velocitat de l'objecte i una altra variable, podeu reordenar la fórmula anterior per trobar la informació desconeguda.
-
Per exemple, diguem que sabem que un tren viatja a 20 quilòmetres per hora durant quatre hores, però no sabem fins on ha recorregut. Per esbrinar-ho, podem reordenar la fórmula de la següent manera:
-
- velocitat = distància / temps
- velocitat × temps = (distància / temps) × temps
- velocitat × temps = distància
- 20 km / hora × 4 hores = distància = 80 quilòmetres
-

Pas 2. Convertiu les unitats que utilitzeu segons calgui
De vegades, podeu calcular la velocitat utilitzant una unitat determinada, però heu de convertir-la en una altra unitat. En aquest cas, heu d’utilitzar un factor de conversió per obtenir la resposta segons les unitats correctes. Per fer-ho, només cal escriure la relació entre les unitats en forma de fracció i multiplicar-la. Quan es multipliqui, invertiu la fracció segons sigui necessari per eliminar les unitats no desitjades. Aquest mètode és molt més fàcil del que sembla.
-
Per exemple, diguem que a l'exemple de problema anterior, necessitem la resposta en milles en lloc de quilòmetres. Una milla equival a uns 1,6 quilòmetres. Per tant, podem fer la conversió de la següent manera:
-
- 80 quilòmetres × 1,6 quilòmetres = 1 milla = 50 milles
-
- Recordeu, perquè els quilòmetres apareixen a la part inferior de la fracció, elimina els quilòmetres de la resposta anterior, de manera que el resultat final fa servir milles.
- Aquest lloc web proporciona funcions de conversió per a la majoria de les unitats d’ús habitual.

Pas 3. Substituïu la variable "distància" per la fórmula de la distància segons calgui
Els objectes no sempre es mouen per un camí recte i suau. Si això és cert, és possible que no pugueu introduir simplement un valor numèric com a unitat de distància a la fórmula de velocitat estàndard. Tanmateix, és possible que hagueu de substituir la lletra j de la fórmula k = j / w per una fórmula que s’assembli a la distància recorreguda per l’objecte.
-
Per exemple, diguem que un avió gira per l'aire una distància de 20 milles 5 vegades. L’avió va completar la ronda en mitja hora. En aquest exemple, encara hem de trobar la distància total recorreguda per l'avió abans de poder determinar-ne la velocitat. Podem utilitzar la fórmula per calcular la distància al voltant d’un cercle (distància al seu voltant) en lloc de j en aquesta fórmula. Aquesta fórmula és circumferència = 2πr on r = radi de circumferència. A continuació s’explica com solucionar-ho:
-
- k = (2 × × r) / w
- k = (2 × × 10) /0,5
- k = 62,83 / 0,5 = 125,66 milles / hora
-

Pas 4. Compreneu que k = j / w dóna la velocitat mitjana
La fórmula senzilla i senzilla que fem servir per trobar la velocitat té un inconvenient. El valor resultant és tècnicament la velocitat mitjana. Això significa que la fórmula suposa que l'objecte que mesureu utilitza la mateixa velocitat que es mou. Com veurem a continuació, trobar la velocitat d’un objecte en un sol moment serà molt més difícil.
Per il·lustrar aquesta diferència, imagineu la darrera vegada que vau viatjar en cotxe. És poc probable que viatgis a la mateixa velocitat que viatges. Tot i així, normalment començareu el viatge a una velocitat baixa i anireu augmentant la velocitat al llarg del camí, aturant-vos a causa de semàfors vermells, embussos, etc. Si utilitzeu la fórmula de velocitat estàndard per trobar la velocitat durant el viatge, no es podran detectar canvis a aquesta velocitat. Tot i això, obtindreu una resposta que mostri la velocitat mitjana de totes les diferències de velocitat que viatgeu
Mètode 3 de 3: càlcul de la velocitat instantània
Nota:
En aquesta secció s’utilitzen tècniques menys familiars per a persones que mai no han estudiat el càlcul. Llegiu els nostres articles sobre càlcul per obtenir ajuda.
Pas 1. Comprendre que la velocitat es defineix com la velocitat d’acceleració
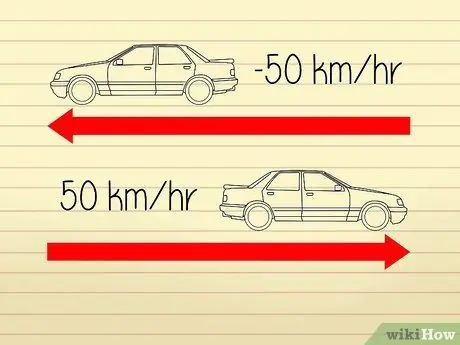
Els càlculs de velocitat d’alt nivell són força confusos perquè matemàtics i científics utilitzen diferents definicions per descriure "velocitat" i "acceleració". L'acceleració té dos components: una "velocitat" i una "direcció". La velocitat és igual a la velocitat de l'objecte. Un canvi de direcció provocarà un canvi d’acceleració, però no un canvi de velocitat.
- Per exemple, diguem que dos cotxes es mouen en direccions oposades. Els velocímetres dels dos cotxes mostren una xifra de 50 km / h, de manera que tots dos viatgen a la mateixa velocitat. Tanmateix, atès que els cotxes s’allunyen els uns dels altres, podem dir que un dels cotxes té una “acceleració” de -50 km / h mentre que l’altre té una “acceleració” de 50 km / h.
- Igual que els càlculs de velocitat instantània, també podeu realitzar càlculs d’acceleració instantània.

Pas 2. Utilitzeu valors absoluts per mesurar l’acceleració negativa
Un objecte pot tenir una velocitat d’acceleració negativa (si es mou en una direcció negativa respecte a un altre objecte). Tot i això, no hi ha velocitat negativa. Així, en aquest cas, el valor absolut de la velocitat indica la velocitat de l’objecte.
Per aquest motiu, a l’exemple anterior, tots dos cotxes tenen una velocitat de 50 km / h.
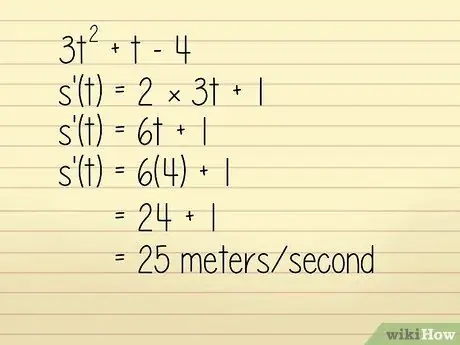
Pas 3. Agafeu la derivada de la posició de la funció
Si teniu una funció k (w) que mostra la posició d’un objecte sense necessitat de calcular el temps, la derivada de k (w) mostrarà l’acceleració sense necessitat de temps. Simplement connecteu el valor del temps a aquesta fórmula perquè la variable w (o el valor del temps que s’utilitzi) s’acceleri segons aquest temps. A partir d’aquí podeu trobar fàcilment la velocitat de l’objecte.
-
Per exemple, diguem que la posició d’un objecte en un metre es descriu a l’equació 3q2 + w - 4 on w = temps en segons. Volem conèixer la velocitat de l'objecte a w = 4 segons. En aquest cas, podeu resoldre-ho mitjançant:
-
- 3w2 + w - 4
- k '(w) = 2 × 3w + 1
- k '(w) = 6w + 1
-
-
Ara, introduïm w = 4:
-
- k '(w) = 6 (4) + 1 = 24 + 1 = 25 metres / segon. Tècnicament es tracta d’un càlcul d’acceleració, però com que és positiva i la direcció no s’esmenta a la pregunta, la podem utilitzar per trobar la velocitat.
-

Pas 4. Preneu la funció d'acceleració integral
L’acceleració és una manera de mesurar el canvi en l’acceleració d’un objecte al llarg del temps. Aquest tema és massa complex per explicar-lo completament en aquest article. Tot i això, és útil tenir en compte que quan teniu una funció a (w) que representa acceleració respecte al temps, la integral de a (w) retornarà el resultat de l’acceleració en funció d’aquest temps. Recordeu, és molt útil conèixer l’acceleració inicial d’un objecte perquè pugueu definir la constant d’aquest resultat a partir d’una integral infinita.
-
Per exemple, diguem que un objecte té una acceleració constant (en m / s2 com a resultat de (w) = -30. Digueu també que l’objecte té una acceleració inicial de 10 m / s. Hem de trobar la velocitat a w = 12 segons. En aquest cas, el podem resoldre mitjançant:
-
- a (w) = -30
- p (w) = a (w) dw = -30dw = -30w + C
-
-
Per trobar C, resoldrem p (w) per w = 0. Recordeu que l’acceleració inicial de l’objecte és de 10 m / s.
-
- p (0) = 10 = -30 (0) + C
- 10 = C, de manera que p (w) = -30w + 10
-
-
Ara podem introduir w = 12 segons.
-
- p (12) = -30 (12) + 10 = -360 + 10 = -350. Com que la velocitat és un valor absolut d’acceleració, la velocitat de l’objecte és 350 metres / segon.
-
Consells
- La pràctica és fantàstica! Intenteu crear la vostra pròpia pregunta substituint els números de l'exemple de problema anterior.
- Si busqueu una manera ràpida de practicar el càlcul per obtenir una millor velocitat de càlcul, utilitzeu la calculadora de derivades en línia aquí i la calculadora integral en línia aquí.






