- Autora Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:11.
- Última modificació 2025-01-23 12:09.
Sumar i restar fraccions és una habilitat important. Les fraccions apareixen a la vida quotidiana tot el temps, especialment a les classes de matemàtiques, des de primària fins a la universitat. Seguiu aquests passos per aprendre a sumar i restar fraccions, de fraccions equivalents, fraccions desiguals, nombres mixts o fraccions comunes. Si ja coneixeu una manera, és molt fàcil resoldre les altres fraccions.
Pas
Mètode 1 de 4: Sumar i restar fraccions amb el mateix denominador
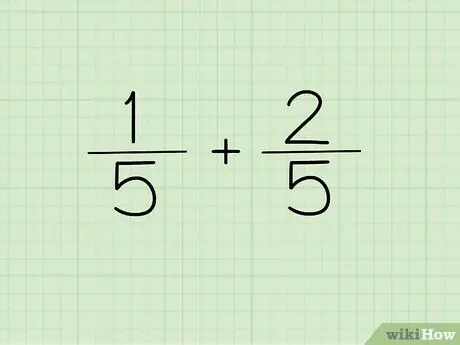
Pas 1. Escriviu la vostra pregunta
Si el denominador de les dues fraccions que voleu sumar o restar és el mateix, escriviu el denominador una vegada com a denominador de la vostra resposta.
En altres paraules, 1/5 i 2/5 no cal escriure's com 1/5 + 2/5 =?, però es pot escriure com (1 + 2) / 5 =?. Els denominadors són els mateixos, de manera que només es poden escriure una vegada. Els dos numeradors es combinen
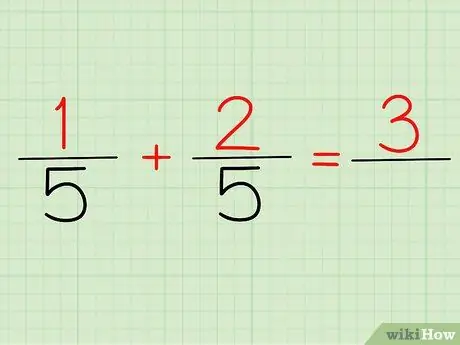
Pas 2. Sumeu els numeradors
El numerador és el nombre que està per sobre de qualsevol fracció. Si observem el problema anterior, 1/5 i 2/5, 1 i 2 són els nostres numeradors.
Tant si ho escriviu 1/5 + 2/5 com (1 + 2) / 5, la vostra resposta serà la mateixa: 3! Perquè, 1 + 2 = 3

Pas 3. Deixeu el denominador
Com que els denominadors són els mateixos, no feu res amb els denominadors. No afegiu, resteu, multipliqueu ni dividiu. Que ho sigui.
Així doncs, a partir del mateix exemple, el nostre denominador és 5. És cert! 5 és el nombre inferior de la nostra fracció. Tenim la meitat de la resposta

Pas 4. Escriviu la vostra resposta
Ara, tot el que heu de fer és escriure el numerador i el denominador. Si utilitzeu l’exemple anterior, la vostra resposta serà 3/5.
Quin és el vostre numerador? 3. El vostre denominador? 5. Per tant, 1/5 + 2/5 o (1 + 2) / 5 és igual a 3/5.
Mètode 2 de 4: Sumar i restar fraccions amb diferents denominadors

Pas 1. Trobeu el mínim comú denominador
És a dir, el denominador més petit és el mateix per a les dues fraccions. Suposem que tenim les fraccions 2/3 i 3/4. Quin és el denominador? 3 i 4. Per trobar el mínim comú denominador de les dues fraccions, podeu fer-ho de tres maneres:
- Anoteu els múltiples de. Els múltiples de 3 són 3, 6, 9, 12, 15, 18 … i així successivament. Múltiples de 4? 4, 8, 12, 16, 20, etc. Quin és el nombre més petit que és múltiple dels dos? 12! Aquest és el denominador menys comú.
-
Factorització primera. Si coneixeu els factors, podeu fer la factorització primera. És a dir, cerqueu els números que formen el vostre denominador. Pel número 3, els factors són 3 i 1. Pel número 4, els factors són 2 i 2. Després, tots vosaltres. 3 x 2 x 2 = 12. El vostre mínim comú denominador!
Multiplicar tots els números pel nombre més petit. En alguns problemes, com aquest, podeu multiplicar els dos números: 3 x 4 = 12. Tanmateix, si teniu un gran denominador, no ho feu! No voleu multiplicar 56 x 44 i fer-ho tot per obtenir 2.464

Pas 2. Multiplicar el denominador pel nombre necessari per obtenir el denominador comú més petit
En altres paraules, voleu que tots els vostres denominadors siguin iguals. En el nostre exemple, volem que el denominador sigui 12. Per canviar de 3 a 12, multiplica 3 per 4. Per canviar de 4 a 12, multiplica 4 per 3. El mateix denominador serà el denominador de la resposta final.
-
Per tant, 2/3 es converteix en 2/3 x 4 i 3/4 es converteix en 3/4 x 3. És a dir, ara tenim 2/12 i 3/12. Però, encara no hem acabat.
- Notareu que els denominadors es multipliquen entre si. Això es pot fer en aquesta situació, però no en totes les situacions. De vegades, en lloc de multiplicar els dos denominadors, podeu multiplicar els dos denominadors per un altre nombre per obtenir el nombre més petit.
- Després, en altres problemes, de vegades només cal multiplicar un denominador per fer-lo igual al denominador de l’altra fracció del problema.

Pas 3. Multiplicar el numerador pel mateix nombre
Quan multipliqueu el denominador per un nombre, també heu de multiplicar el numerador pel mateix nombre. El que vam fer a l’últim pas és només una part de la multiplicació que s’ha de fer.
Tenim 2 / 3x4 i 2 / 4x3 com a primer pas; després, al segon pas, 2 x 4/3 x 4 i 3 x 3/4 x 3. És a dir, els nostres nous números són 8/12 i 9 / 12. Perfecte
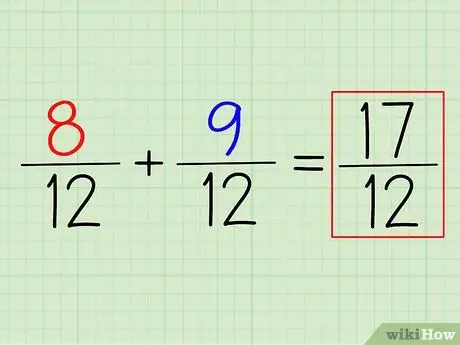
Pas 4. Afegiu (o resteu) els numeradors per obtenir la resposta
Per afegir 8/12 + 9/12, només cal que sumeu els numeradors. Recordeu: només heu de deixar el denominador. El denominador comú més petit que trobeu és el vostre denominador final.
En aquest exemple, (8 + 9) / 12 = 17/12. Per convertir-lo en un nombre mixt, només cal restar el denominador del numerador i escriure la resta. En aquest cas, 17/12 = 1 5/12
Mètode 3 de 4: sumar i restar fraccions mixtes i comunes
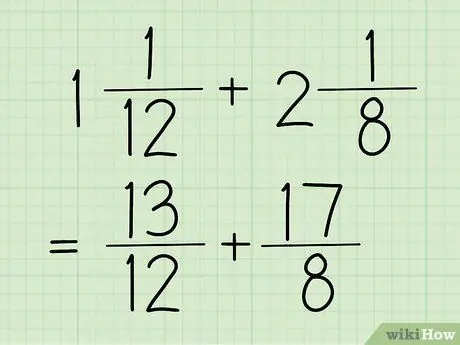
Pas 1. Converteix les fraccions mixtes en fraccions comunes
Un nombre mixt és una fracció que té un nombre enter i una fracció, com en l'exemple anterior (1 5/12). Mentrestant, una fracció ordinària és una fracció el numerador del qual (nombre superior) és superior al denominador (nombre inferior). Aquesta fracció també es veu al pas anterior, que és el 17/12.
Per als exemples d’aquesta secció, utilitzarem el 13/12 i el 17/8

Pas 2. Cerqueu un denominador comú
Recordeu les tres maneres de trobar el mínim comú denominador? Escrivint múltiples, utilitzant la factorització primera o multiplicant els denominadors.
Trobem múltiples del nostre exemple, 12 i 8. Quin és el nombre més petit que tenen tots dos en comú? 24. 8, 16, 24 i 12, 24: bingo

Pas 3. Multipliqueu el numerador i el denominador per trobar la fracció equivalent
Cal canviar els dos denominadors a 24. Com es converteix 12 a 24? Multiplicar per 2. 8 a 24? Multiplicar per tres. Però no ho oblideu: també heu de multiplicar els numeradors.
Per tant (13 x 2) / (12 x 2) = 26/24. I (17 x 3) / (8 x 3) = 51/24. Gairebé hem acabat amb això

Pas 4. Sumeu o resteu les vostres fraccions
Ara que teniu el mateix denominador, podeu afegir fàcilment els dos numeradors. Recordeu, només heu de deixar el denominador.
26/24 + 51/24 = 77/24. Aquesta és la vostra suma! Tot i això, els números a la part superior eren massa grans …

Pas 5. Torneu a convertir la vostra resposta en nombres mixtos
El nombre molt gran que hi ha a la part superior de la fracció sembla una mica estrany: no es pot saber la mida de la fracció. Tot el que heu de fer és restar el denominador del numerador repetidament fins que no es pugui restar més i anotar la resta.
-
En aquest exemple, 77 menys 24 per 3 vegades. És a dir, 24 x 3 = 72. La resta és 5! Quin és el vostre resultat final? 3 5/24.
Tan cert!
Mètode 4 de 4: sumar i restar fraccions sense trobar LCM
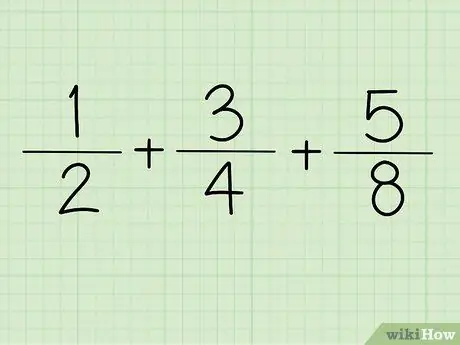
Pas 1. Anota la fracció
Per exemple + +

Pas 2. Resol primer el numerador
- Multiplicar pel numerador de l'altra fracció.
- Multiplicar 1 per 4 i 8. [32]
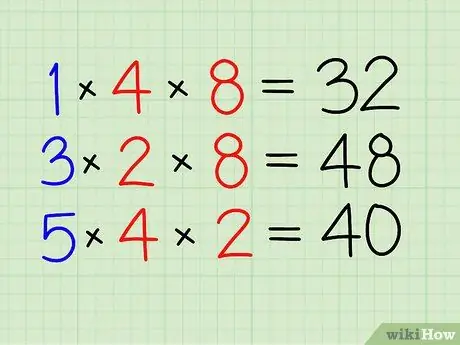
Pas 3. Feu el mateix per a les altres fraccions
- Multiplicar 3 per 2 i 8. [48]
- Finalment, multiplica 5 per 4 i 2. [40]
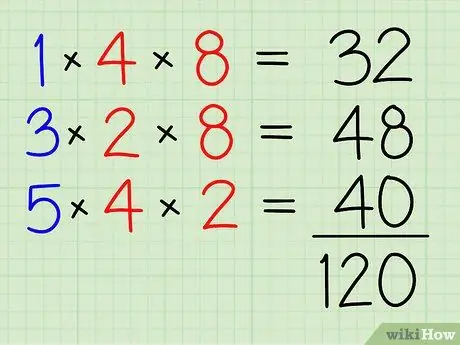
Pas 4. Afegiu-los tots junts
32+48+40=120
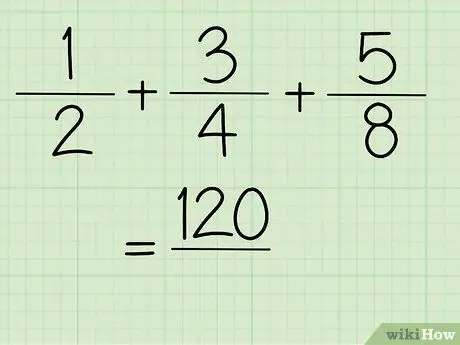
Pas 5. Ara, obteniu el valor del numerador

Pas 6. Resol el denominador de la fracció

Pas 7. Multiplicar tots els denominadors de les fraccions
2×4×8=64

Pas 8. Ara obtindreu el resultat
120/64 = 1 56/64 = 1 ⅞
Advertiment
- Aquest mètode permet multiplicar nombres grans.
- És possible que necessiteu una calculadora per calcular aquesta manera.






