- Autora Jason Gerald [email protected].
- Public 2024-01-15 08:11.
- Última modificació 2025-01-23 12:10.
Podríeu pensar que els enters són només nombres ordinaris, com 3, -12, 17, 0, 7000 o -582. Els enters també s’anomenen nombres enters perquè no es divideixen en parts com fraccions i decimals. Llegiu aquest article per aprendre tot el que necessiteu per afegir i restar enters, o bé llegiu directament la secció que necessiteu.
Pas
Mètode 1 de 5: sumar i restar nombres enters positius mitjançant una línia numèrica

Pas 1. Comprendre la línia numèrica
Les línies numèriques converteixen les matemàtiques bàsiques en quelcom tangible i físic que podeu veure. Amb només uns quants signes i sentit comú, el podem utilitzar com una calculadora per sumar i restar nombres.

Pas 2. Dibuixeu una línia numèrica base
Imagineu o traqueu una línia recta parella. Feu un punt al mig de la línia. Escriu 0 o zero al costat d’aquest període.
El vostre llibre de matemàtiques podria anomenar-ho el punt de partida perquè és el punt de partida de tots els números

Pas 3. Dibuixa dos punts, un a la dreta i a l’esquerra del zero
Escriu - 1 al costat del punt de l'esquerra i
Pas 1. al costat del punt de la dreta. Aquest és l’enter més proper a zero.
- No us preocupeu per fer les distàncies entre els punts exactament iguals, sempre que sàpiga què significa cada punt, es pot utilitzar una línia numèrica.
- El costat esquerre és el començament de la frase.

Pas 4. Completeu la línia numèrica afegint més números
Feu més punts a l'esquerra que -1 i a la dreta que 1. A l'esquerra, des de -1, marqueu els punts amb - 2, - 3, i - 4. A la dreta, des de l'1, marqueu el punt amb
Pas 2
Pas 3., da
Pas 4.. Podeu continuar si teniu espai al vostre paper.
L'exemple de la figura mostra una línia numèrica de -6 a 6

Pas 5. Comprendre els nombres enters positius i negatius
Nombres enters positius, també anomenats nombre natural, és un nombre enter superior a zero. 1, 2, 3, 25, 99 i 2007 són nombres enters positius. Els enters negatius són enters que són inferiors a zero (com ara -2, -4 i -88).
Els enters són una altra forma de trucar a nombres enters. Les fraccions com 1/2 (la meitat) només són una part del nombre, de manera que no són enters. Igual que decimal, per exemple 0,25 (punt zero dos cinc); decimal no és un nombre enter

Pas 6. Comenceu a resoldre 1 + 2 col·locant el dit al punt 1
Resoldrem problemes d’addició senzills 1+2 mitjançant la línia numèrica que acabeu de crear. El primer número és
Pas 1., així que comenceu a posar el dit al número.
-
És massa fàcil aquesta pregunta?
Si heu afegit alguna vegada, probablement sabreu la resposta a l’1 + 2. Bé: si coneixeu el resultat, serà més fàcil entendre com funciona la línia numèrica. A continuació, podeu utilitzar la línia numèrica per resoldre problemes d’addició més difícils o preparar-vos per a matemàtiques més difícils com l’àlgebra.

Pas 7. Sumeu 1 + 2 movent el dit 2 punts cap a la dreta
Feu lliscar el dit cap a la dreta, comptant el nombre de punts (un altre número) que passeu. Si heu superat 2 punts nous, atureu-vos. El número que assenyala el dit és la resposta,
Pas 3
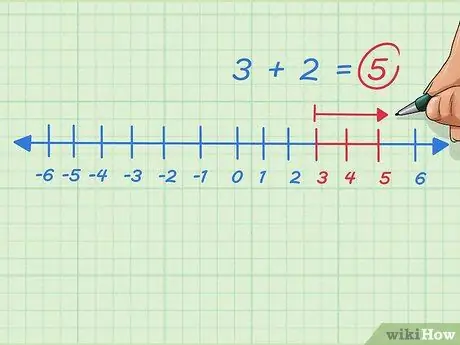
Pas 8. Afegiu els nombres enters positius movent-vos cap a la dreta a la línia numèrica
Suposem que volem resoldre 3 + 2. Comenceu per les 3, moveu-vos a la dreta o afegiu 2 punts. Ens aturem a 5. El problema s’escriu 3 + 2 = 5.

Pas 9. Resteu nombres enters positius movent-vos a l'esquerra sobre la línia numèrica
Per exemple, volem resoldre 6 -4, comencem per 6, ens desplacem cap a l'esquerra 4 punts i parem a 2. Aquest problema està escrit 6 - 4 = 2.
Mètode 2 de 5: sumar i restar números negatius mitjançant una línia numèrica

Pas 1. Més informació sobre les línies numèriques
Si no sabeu com crear una línia numèrica, torneu a la secció Suma i resta de números positius mitjançant línies numèriques per obtenir informació sobre com crear-ne una.
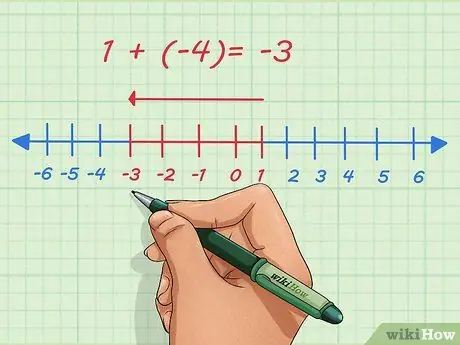
Pas 2. Comprendre els números negatius
Els números positius s’indiquen amb la direcció de la dreta a la línia numèrica. Els números negatius s’indiquen a l’esquerra a la línia numèrica. Afegir números negatius significa moure el punt cap a l’esquerra de la línia numèrica.
-
Per exemple, afegim 1 i -4. Normalment, aquesta pregunta s’escriu així:
1 + (-4)
. A la línia numèrica, comencem per 1, ens movem 4 punts cap a l'esquerra i parem a -3.
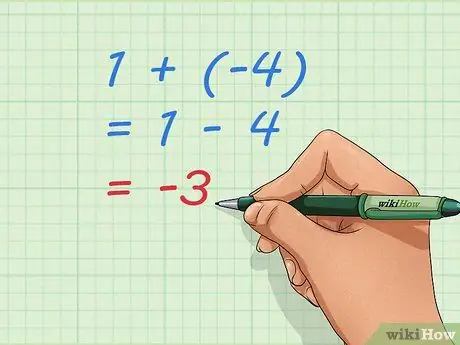
Pas 3. Utilitzeu equacions bàsiques per entendre l’addició de nombres negatius
Fixeu-vos que -3, la nostra resposta, és el número que obtindrem si fem 1 - 4. Sumar 1 + (-4) i restar 4 d'1 és el mateix problema. El podem escriure com una equació, una frase matemàtica que mostra igualtat: 1 + (-4) = 1 - 4 = -3
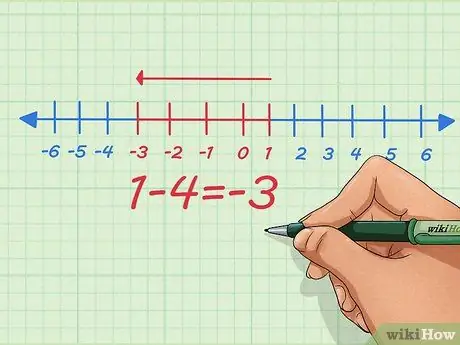
Pas 4. En lloc d’afegir nombres negatius, converteix-lo en un problema de resta mitjançant números positius
Com podem veure a la simple equació anterior, podem fer les dues coses: convertir l'addició de nombres negatius en resta de nombres positius i viceversa. És possible que us hagin ensenyat a convertir els negatius en negatius sense saber per què: aquí teniu el perquè.
-
Per exemple, -4. Quan sumem -4 i 1, restem 1 per 4. Es pot escriure en matemàtiques escrivint
1 + (-4) = 1 - 4
. Podem escriure-ho a la línia numèrica, començant pel nostre punt inicial a 1 i afegint 4 punts a l'esquerra (és a dir, afegint -4). Com que es tracta d’una equació, una cosa és igual a una altra, de manera que també és cert el contrari
1 - 4 = 1 + (-4)
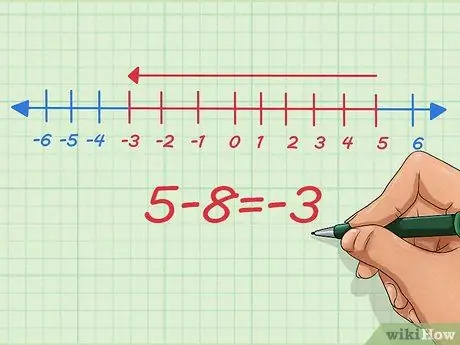
Pas 5. Compreneu com restar nombres negatius en una línia numèrica
A la línia numèrica, restar números negatius és el mateix que reduir la longitud. Comencem per 5 - 8.
A la línia numèrica, comencem al nostre punt inicial a 5, restem 8 i ens aturem a -3
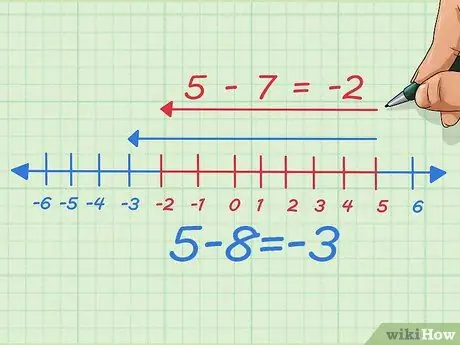
Pas 6. Resteu la quantitat que esteu restant i vegeu què passa
Suposem que restem un, el nombre que restem o, dit d’una altra manera, restem 7 en lloc de 8. Ara restem un punt a l’esquerra de la línia numèrica. Per escrit, vam començar amb 5 - 8 = -3 Ara, només movem 7 a l’esquerra, de manera que es converteix en 5 - 7 = -2
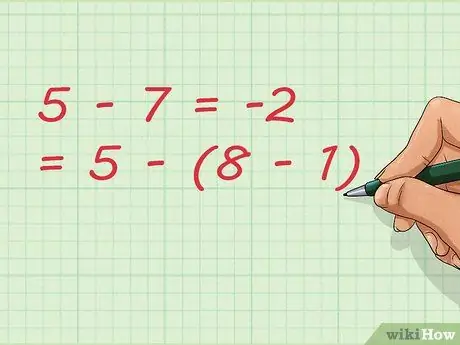
Pas 7. Fixeu-vos que la resta també pot resultar
En el nostre exemple, restem el número 1. En escriure l’equació, podem escriure-la més curta com: 5 - 7 = -2 = 5 - (8 - 1)

Pas 8. Converteix els signes negatius en positius en afegir nombres negatius
Mitjançant el pas de convertir totes les restes en sumes, podem escriure-les més curtes com: 5 - (8 - 1) = 5 - 7 = 5 - 8 + 1.
-
Ja sabem que 5-8 = -3, per tant, traieu 5-8 de l’equació i introduïu -3:
5 - (8 - 1) = 5 - 7 = -3 + 1
-
Ja sabem que 5 - (8 - 1) és - resta un punt de 5 - 8. La nostra equació pot mostrar que 5 - 8 és igual a -3 i restar un punt dóna -2. L'equació es pot escriure així:
-3 - (-1) = -3 + 1
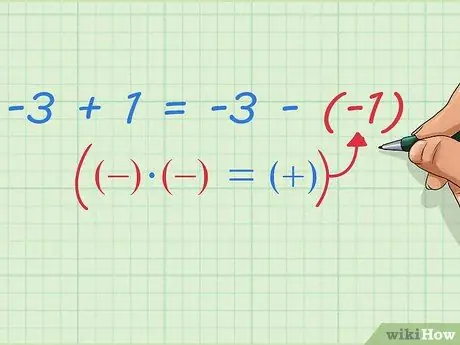
Pas 9. Escriviu la resta de nombres negatius com a suma
Fixeu-vos què passa després d'això: ja hem demostrat que: -3 + 1 = -3 - (-1) Podem escriure això amb regles d'escriptura matemàtica més senzilles i generals: primer número més segon número = primer número menys (segon número negatiu) O una manera més senzilla que probablement heu sentit a la classe de matemàtiques: Canvieu els dos signes negatius per un signe positiu.
Mètode 3 de 5: afegir enters enters positius

Pas 1. Escriviu el problema de suma de 2.503 + 7.461 amb un número sobre l'altre
Anoteu els números a la columna gran de manera que 2 sigui superior a 7, 5 sigui superior a 4, etc. D’aquesta manera, aprendrem a afegir nombres enters massa grans per imaginar o utilitzar la línia numèrica.
Escriviu un signe + a l’esquerra del número de sota i la línia que hi ha a sota, ja que podríeu aprendre per a problemes d’addició més petits
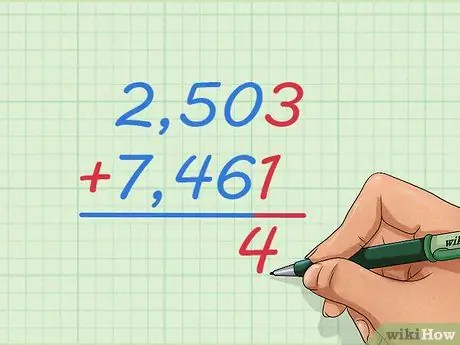
Pas 2. Comenceu sumant els dos números a l'extrem dret
Podria ser una mica estrany començar per la dreta perquè llegim números des de l’esquerra. Hem d’afegir des de la dreta per obtenir la resposta correcta, que podreu veure més endavant.
-
Sota els dos números més a la dreta,
Pas 3. da
Pas 1., escriviu la suma dels dos
Pas 4..

Pas 3. Sumeu cada número a la columna de la mateixa manera
Moveu-vos cap a l’esquerra, sumeu 0+6, 5+4, i 2+7. Escriviu la resposta sota cada parell de números.
La vostra resposta hauria de ser: 9.964. Comproveu el vostre treball si cometeu un error.

Pas 4. Ara suma 857 + 135
Notareu alguna cosa diferent tan aviat com afegiu el primer parell de números a la dreta. 7+5 és igual a 12, un número de dos dígits, però només podeu escriure un dígit sota aquesta columna. Seguiu llegint per saber què heu de fer i per què heu de començar sempre per la dreta i no per l’esquerra.

Pas 5. Sumeu 7 + 5 i apreneu on escriure la resposta
7 + 5 = 12, però no es pot posar 1 i 2 sota la línia. Però, escriviu l'últim dígit, Pas 2., sota la línia i anota el primer dígit
Pas 1., a sobre de la columna a l'esquerra, 5 + 3.
-
Si teniu curiositat per com funciona, penseu en què significa dividir 1 i 2. De fet, en esteu dividint 12 en
Pas 10. da
Pas 2.. Podeu escriure 10 per sobre del número si voleu i veureu 1 a les columnes 5 i 3, igual que abans.

Pas 6. Sumeu 1 + 5 + 3 per obtenir el següent dígit de la resposta
Ara teniu tres dígits per afegir perquè n'heu afegit 1 a aquesta columna. La resposta és
Pas 9., de manera que la vostra resposta esdevé 92.
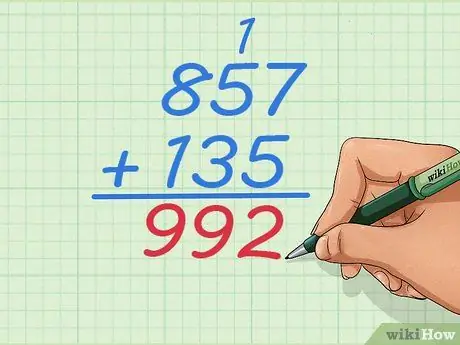
Pas 7. Completeu el problema com de costum
Continueu treballant els dígits cap a l'esquerra fins que sumeu tots els números; en aquest cas, només queda una columna. La resposta final hauria de ser 992.
- Podeu provar preguntes més complicades, com ara 974 + 568. Recordeu, sempre que obtingueu un número de dos dígits, només escriviu l’últim dígit com a resposta i col·loqueu l’altre dígit a sobre de la columna a l’esquerra, que sumareu a continuació. Si la resposta de l'última columna (a l'esquerra) conté dos dígits, escriviu-la com a resposta.
- Consulteu la secció de Consells per obtenir respostes a les preguntes 974 + 568 un cop provades a resoldre-les.
Mètode 4 de 5: restar enters enters positius

Pas 1. Escriviu el problema de la resta 4.713 - 502 amb el primer número a sobre del segon número
Escriviu-lo de manera que 3 estigui directament per sobre de 2, 1 sigui superior a 0, 7 estigui per sobre de 5 i 4 estigui per sobre del blanc.
Podeu escriure de 0 a 4 si això us ajuda a recordar quin número està per sobre de quin número. Sempre podeu afegir un 0 davant d’un número sense canviar-lo. Assegureu-vos d’afegir-lo abans del número i no després

Pas 2. Resteu cada número següent del número que hi ha directament a sobre
Comenceu sempre per la dreta. Resoleu 3-2, 1-0, 7-5 i 4-0, escriviu la resposta a cada pregunta directament a sota dels dos números restats.
El resultat és, 4.211.

Pas 3. Ara escriviu les preguntes 924-518 de la mateixa manera
Aquests números tenen el mateix nombre de dígits, de manera que els podeu escriure fàcilment. Aquest problema us ensenyarà a restar enters si encara no ho sabeu.

Pas 4. Apreneu a resoldre el primer problema, que es troba a l’extrema dreta
4 - 8. Aquest problema és complicat perquè 4 és inferior a 8, però no utilitzeu números negatius, però seguiu aquests passos:
- A la fila superior, creueu 2 i escriviu 1. 2 ha d’estar a l’esquerra de 4.
- Creueu 4 i escriviu 14. Feu-ho en un espai estret per tal que quedi clar que 14 supera 8. També podeu escriure 1 davant de 4 per fer 14 si hi ha prou espai.
- El que acabeu de fer és agafar 1 del lloc de les desenes o la segona columna de la dreta i convertir-lo a 10 al lloc o a la columna de l'extrema dreta. Una vegada que el número 10 és igual a deu vegades el número 1, és igual.

Pas 5. Ara resoleu els problemes 14 - 8 i escriviu la resposta a la columna de la dreta
Hauria d’haver escrit 6 a la línia de resposta més a la dreta.

Pas 6. Completeu la següent columna a l'esquerra amb el número nou que heu escrit
La resta ha de ser 1 - 1, que és igual a 0.
La vostra resposta ara hauria de ser 06.

Pas 7. Resoleu el problema completant l'última resta, la columna més a l'esquerra
9 - 5 = 4, de manera que la resposta final és 406.

Pas 8. Ara resolem el problema de restar nombres grans de nombres petits
Suposem que se us demana que completeu 415.990 - 968.772. Escriviu el segon número sota el primer número i us adonareu que el número següent és més gran. Es pot saber immediatament des del primer dígit de l’esquerra: 9 és més gran que 4, de manera que els números que comencen per 9 són més grans.
Assegureu-vos d’escriure correctament la columna abans de comparar-la. 912 no superior a 5000, podeu saber si escriviu correctament la columna perquè no hi ha números inferiors a 5. Podeu afegir ajuda zero, per exemple, escriviu 912 amb 0912 perquè la columna sigui igual a 5000.

Pas 9. Escriviu el nombre més petit sota el nombre més gran i afegiu un signe - davant de la resposta
Sempre que resteu un número d’un nombre més petit, el resultat és un nombre negatiu. És millor escriure aquest signe abans de restar perquè no us oblideu d’escriure-ho.

Pas 10. Per respondre, resteu el nombre petit del gran nombre i recordeu d’escriure el signe -
La vostra resposta serà negativa, cosa que s’indica amb un signe -. No ho feu intenta restar un gran nombre d'un nombre petit i després fa que el resultat sigui negatiu; la teva resposta serà errònia.
El nou problema a resoldre és: 968.772 - 415.990 = -? Consulteu la secció de Consells per obtenir la resposta després d’intentar resoldre aquest problema
Mètode 5 de 5: sumar i restar nombres enters negatius
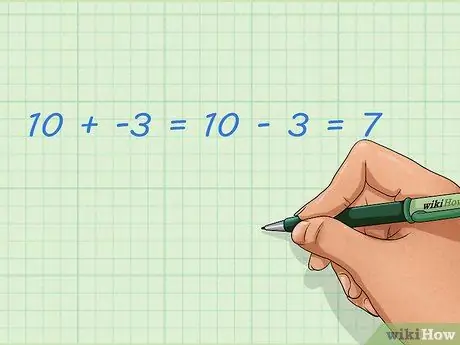
Pas 1. Apreneu a afegir nombres negatius i positius
Sumar nombres enters negatius és el mateix que restar nombres enters positius. Això és més fàcil de fer amb la línia numèrica descrita en una altra secció, però també ho podeu pensar amb paraules. Els nombres negatius no són nombres ordinaris; aquest nombre és inferior a zero i pot representar la quantitat presa. Si afegiu aquesta captura a un número normal, el resultat es reduirà.
- Exemple: 10 + -3 = 10 - 3 = 7
- Exemple: -12 + 18 = 18 + -12 = 18 - 12 = 6. Recordeu que sempre podeu canviar l'ordre dels nombres a més, però no per restar.
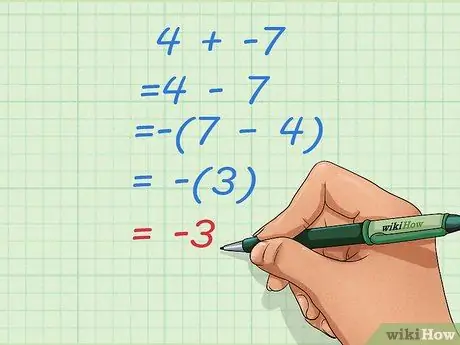
Pas 2. Apreneu què heu de fer si el convertiu en un problema de resta amb un número inicial més petit
De vegades, canviar la suma de problemes de restes com l’anterior pot provocar respostes estranyes com el 4 al 7. Quan això passi, inverteix l’ordre dels nombres i fa que el resultat sigui negatiu.
- Suposem que el vostre problema inicial és 4 + -7.
- Converteix-lo en un problema de resta: 4-7
- Invertiu l'ordre i feu que el resultat sigui negatiu: - (7 - 4) = - (3) = -3.
- Si no esteu familiaritzat amb l'ús de claudàtors en equacions, penseu en això: 4 - 7 es converteix en 7 - 4 amb l'addició d'un signe negatiu. 7 - 4 = 3, però l’hem de canviar per -3 perquè la resposta a les preguntes 4 - 7 sigui correcta.
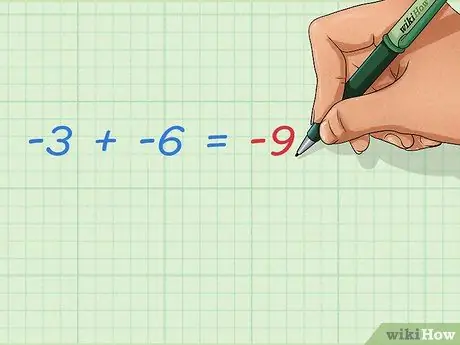
Pas 3. Apreneu a afegir dos enters negatius
Dos nombres negatius afegits sempre fan que el resultat negatiu sigui més gran. Com que no s’afegeixen nombres positius, el resultat estarà més lluny de 0. La resposta és fàcil:
- -3 + -6 = -9
- -15 + -5 = -20
- Veieu el patró? Tot el que heu de fer és sumar els números com si fossin nombres positius i afegir un signe negatiu. -4 + -3 = - (4 + 3) = -7
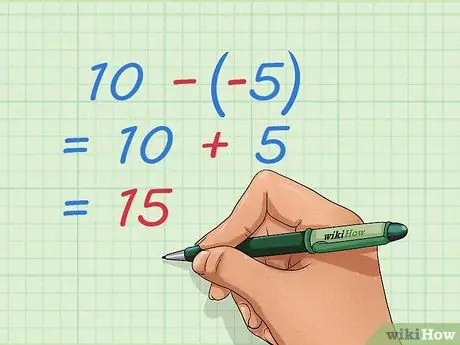
Pas 4. Apreneu a restar enters enters negatius
Igual que el problema de l’addició, podeu reescriure el problema de manera que només tingueu números positius. Si resteu nombres negatius, traieu algunes de les coses que ja s’han pres, que és el mateix que afegir nombres positius.
- Penseu en els números negatius com a diners robats. Si restes o treus diners robats per tornar-los, és com donar diners a algú, oi?
- Exemple: 10 - -5 = 10 + 5 = 15
- Exemple: -1 - -2 = -1 + 2. Ja heu après a resoldre aquest problema al primer pas, recordeu? Torneu a llegir com afegir números negatius i positius si ho oblideu.
- Aquí teniu la solució completa de l’últim exemple: -1 - -2 = -1 + 2 = 2 + -1 = 2 - 1 = 1.
Consells
- És possible que hàgiu escrit números llargs com 2.521.301 amb comes (,) en lloc de (.) Segons el lloc on visqueu. Utilitzeu allò que el professor us demani perquè no us confongueu amb altres sistemes d’escriptura.
- Dibuixa les teves línies numèriques en diferents escales per representar diferents nombres. No hi ha cap regla que cada distància d'una línia numèrica sigui igual a 1. Imagineu una línia numèrica que sigui 10 en lloc de 1. A part del fet que cada punt és 10 ara, la suma i la resta segueixen sent les mateixes. Proveu-ho si no us ho creieu.
- Si proveu les preguntes de desafiament especials a la secció Números llargs, aquí teniu la resposta: 974 + 568 = 1.542. La resposta entre 415.990 i 968.772 és - 552.782.






