- Autora Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:11.
- Última modificació 2025-01-23 12:10.
La força normal és la magnitud de la força necessària per negar les altres forces en qualsevol escenari. La millor manera de trobar-lo depèn de l'estat de l'objecte i de les variables que tingueu. Seguiu llegint per obtenir més informació.
Pas
Mètode 1 de 5: estil normal en repòs
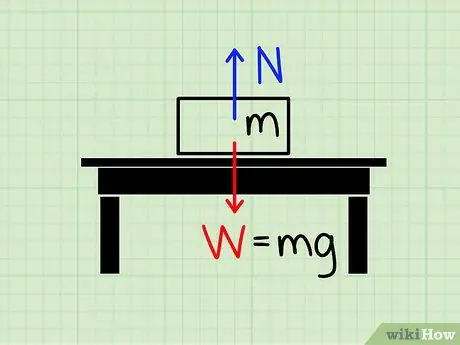
Pas 1. Comprendre el significat de la força normal
La força normal es refereix a la magnitud de la força utilitzada per negar la força gravitatòria.
Imagineu-vos un bloc en repòs sobre una taula. La força de la gravetat arrossega el bloc cap a la terra, però és evident que hi ha una força que impedeix que el bloc aixafi la taula i caigui a terra. Es diu la força que actua per aturar aquest bloc malgrat la força de la gravetat estil normal.
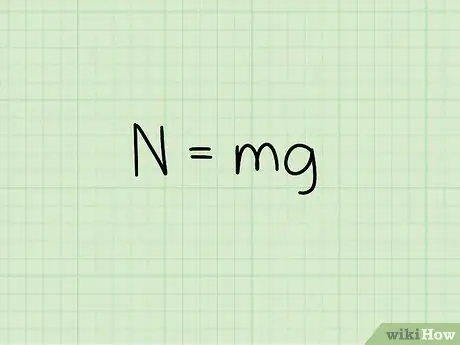
Pas 2. Conegueu l'equació de la força normal sobre un objecte en repòs
Quan calculeu la força normal d’un objecte quan es troba en repòs sobre una superfície plana, utilitzeu la fórmula: N = m * g
- En aquesta equació, N simbolitza l’estil normal, m representa la massa de l'objecte i g representa l’acceleració deguda a la gravetat.
- Per a un objecte que està en repòs sobre una superfície plana, sense que actuï una força externa, la força normal és igual al pes de l'objecte. Per mantenir un objecte en repòs, la força normal ha de ser igual a la força gravitatòria que actua sobre l’objecte. La força gravitatòria que actua sobre un objecte és el pes de l’objecte, o la massa de l’objecte multiplicada per l’acceleració deguda a la gravetat.
- Exemple: trobeu la força normal d’un bloc amb una massa de 4,2 kg.
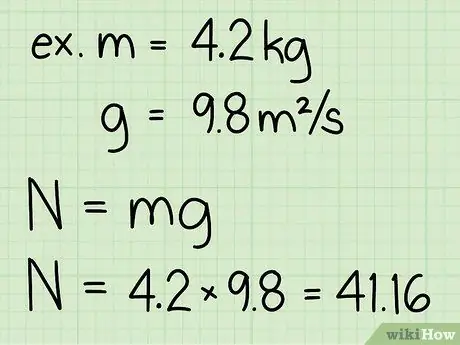
Pas 3. Multiplicar la massa de l'objecte i l'acceleració deguda a la gravetat
Aquesta multiplicació produirà el pes de l'objecte, que per descomptat és igual a la força normal de l'objecte en repòs.
- Tingueu en compte que l’acceleració a causa de la gravetat a la superfície terrestre sempre és constant: g = 9,8 m / s2
- Exemple: pes = m * g = 4, 2 * 9, 8 = 41, 16

Pas 4. Escriviu les respostes
El pas anterior solucionarà el problema i us donarà la vostra resposta.
Exemple: la força normal és 41, 16 N
Mètode 2 de 5: Força normal sobre un pla inclinat
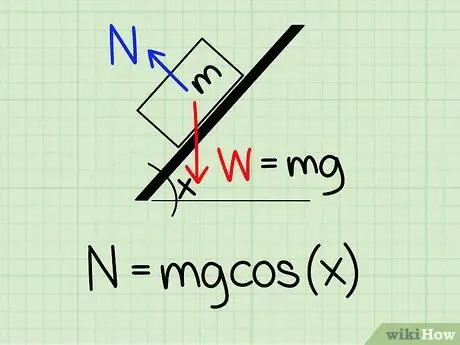
Pas 1. Utilitzeu l'equació correcta
Per calcular la força normal sobre un objecte inclinat per un angle determinat, heu d’utilitzar la fórmula: N = m * g * cos (x)
- Per a aquesta equació, N simbolitza l’estil normal, m representa la massa de l'objecte g representa l’acceleració deguda a la gravetat i x representa l’angle oblic.
- Exemple: trobeu la força normal d’un bloc amb una massa de 4,2 kg, que descansa sobre un pla inclinat amb una inclinació de 45 graus.

Pas 2. Trobeu el cosinus de l'angle
El cosinus de l’angle és igual al sinus de l’angle complementari, o el costat adjacent dividit per la hipotenusa del triangle format pel pendent.
- Aquest valor es determina sovint amb una calculadora perquè el cosinus de qualsevol angle sempre és constant, però també es pot calcular manualment.
- Exemple: cos (45) = 0,71
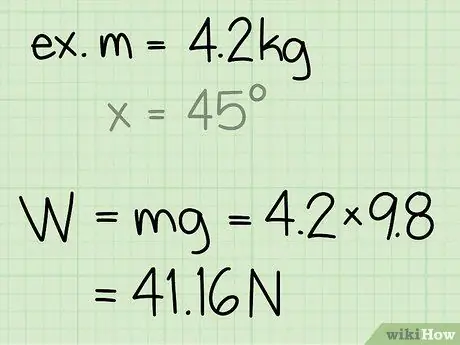
Pas 3. Trobeu el pes de l'objecte
El pes d’un objecte és igual a la massa de l’objecte multiplicada per l’acceleració per gravetat.
- Tingueu en compte que l’acceleració a causa de la gravetat a la superfície terrestre sempre és constant: g = 9,8 m / s2
- Exemple: pes = m * g = 4, 2 * 9, 8 = 41, 16
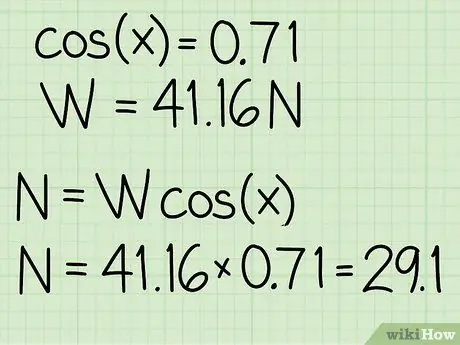
Pas 4. Multipliqueu els dos valors
Per trobar la força normal, heu de multiplicar el pes de l’objecte pel cosinus de l’angle d’inclinació.
Exemple: N = m * g * cos (x) = 41, 16 * 0, 71 = 29, 1
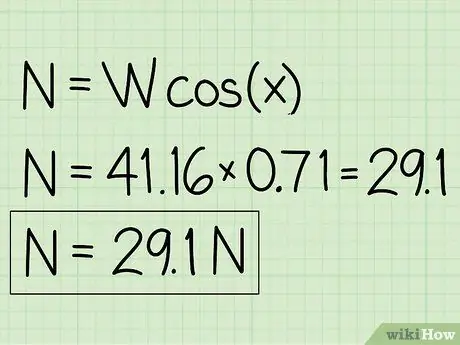
Pas 5. Escriviu les respostes
El pas anterior solucionarà el problema i us proporcionarà la resposta.
- Tingueu en compte que quan un objecte està en repòs sobre una inclinació, la força normal serà inferior al pes de l'objecte.
- Exemple: la força normal és 29,1 N.
Mètode 3 de 5: estil normal amb estil exterior cap avall
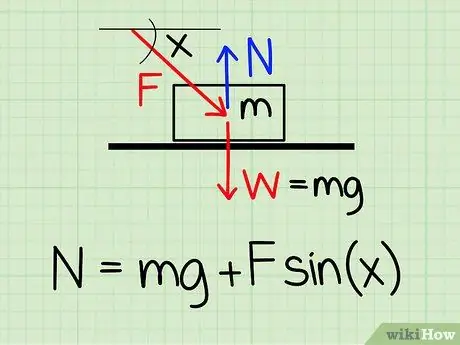
Pas 1. Utilitzeu l'equació correcta
Per calcular la força normal sobre un objecte en repòs si hi ha una força externa descendent sobre l’objecte, utilitzeu l’equació: N = m * g + F * sin (x) '
- N simbolitza l’estil normal, m representa la massa de l'objecte g representa l’acceleració deguda a la gravetat, F simbolitza l'estil extern i x representa l’angle entre l’objecte i la direcció de la força externa.
- Exemple: trobeu la força normal d'un objecte amb una massa de 4,2 kg si l'objecte és empès per una persona amb un angle de 30 graus i una força de 20,9 N.
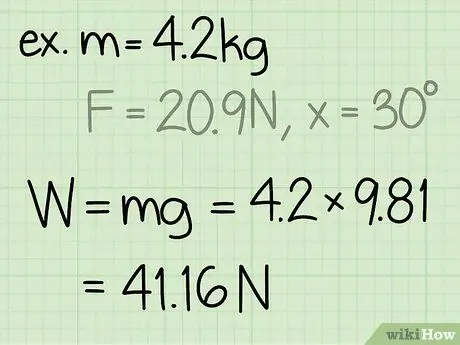
Pas 2. Cerqueu el pes de l'objecte
El pes d’un objecte és igual a la massa de l’objecte multiplicada per l’acceleració per gravetat.
- Tingueu en compte que l’acceleració a causa de la gravetat a la superfície terrestre sempre és constant: g = 9,8 m / s2
- Exemple: pes = m * g = 4, 2 * 9, 8 = 41, 16
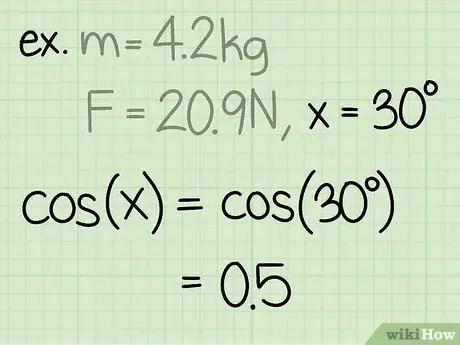
Pas 3. Trobeu el sinus de l'angle
El sinus d’un angle es calcula dividint el costat del triangle oposat a l’angle, per la hipotenusa de l’angle.
Exemple: sin (30) = 0,5

Pas 4. Multiplicar el sinus per la força externa
La força externa, en aquest exemple, fa referència a la força descendent que colpeja l'objecte.
Exemple: 0, 5 * 20, 9 = 10, 45
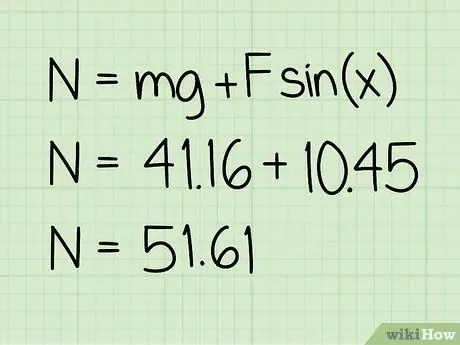
Pas 5. Afegiu aquest valor al pes
Aquesta suma donarà la magnitud de la força normal que actua.
Exemple: 10, 45 + 41, 16 = 51, 61
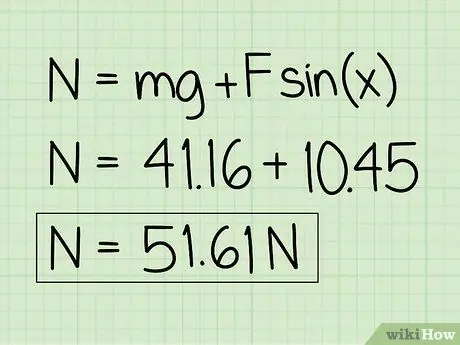
Pas 6. Escriviu les respostes
Tingueu en compte que per a un objecte en repòs afectat per una força descendent externa, la força normal serà superior al pes de l'objecte.
Exemple: la força normal és 51,61 N
Mètode 4 de 5: estil normal amb estil exterior cap amunt
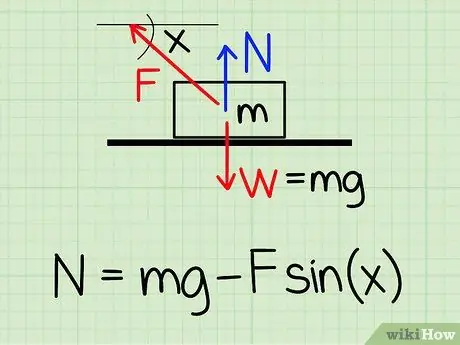
Pas 1. Utilitzeu l'equació correcta
Per calcular la força normal sobre un objecte en repòs si hi ha una força exterior ascendent sobre l’objecte, utilitzeu l’equació: N = m * g - F * sin (x) '
- N simbolitza l’estil normal, m representa la massa de l'objecte g representa l’acceleració deguda a la gravetat, F simbolitza l'estil extern i x representa l’angle entre l’objecte i la direcció de la força externa.
- Exemple: trobeu la força normal d'un bloc amb una massa de 4,2 kg, si algú estira el bloc amb un angle de 50 graus i una força de 20,9 N.

Pas 2. Cerqueu el pes de l'objecte
El pes d’un objecte és igual a la massa de l’objecte multiplicada per l’acceleració per gravetat.
- Tingueu en compte que l’acceleració a causa de la gravetat a la superfície terrestre sempre és constant: g = 9,8 m / s2
- Exemple: pes = m * g = 4, 2 * 9, 8 = 41, 16
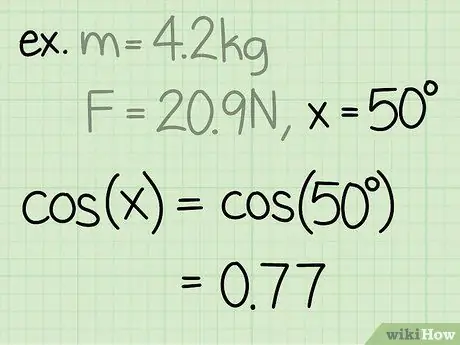
Pas 3. Trobeu el sinus de l'angle
El sinus d’un angle es calcula dividint el costat del triangle oposat a l’angle, per la hipotenusa de l’angle.
Exemple: sin (50) = 0, 77

Pas 4. Multiplicar el sinus per la força externa
La força externa es refereix a la força ascendent que colpeja l'objecte, en aquest cas.
Exemple: 0,77 * 20, 9 = 16, 01
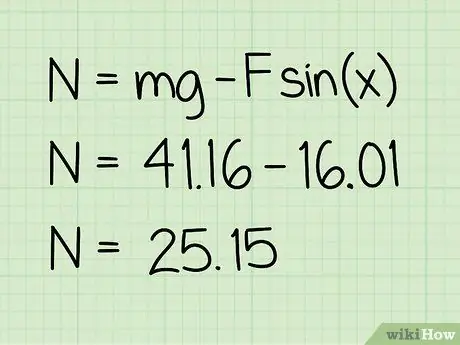
Pas 5. Resteu aquest valor del pes
La resta que feu us donarà la magnitud de la força normal que hi actua.
Exemple: 41, 16 - 16, 01 = 25, 15
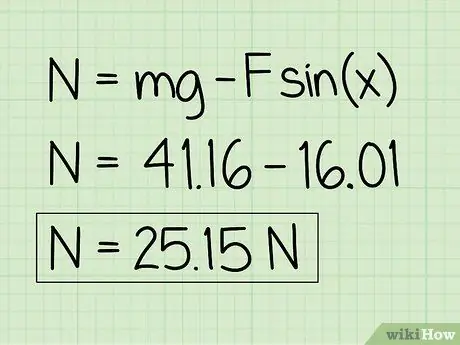
Pas 6. Escriviu les respostes
Tingueu en compte que un objecte en repòs es veu afectat per una força externa ascendent, la força normal serà inferior al pes de l'objecte.
Exemple: la força normal és 25, 15 N
Mètode 5 de 5: força normal i fregament

Pas 1. Conegueu l'equació bàsica per a la fricció cinètica
La fricció cinètica, o fricció d’un objecte en moviment, és igual al coeficient de fricció multiplicat per la força normal d’un objecte. En forma d'equació: f = * N
- En aquesta equació, f simbolitzar la fricció, ️ representa el coeficient de fricció i N representa la força normal de l'objecte.
- El "coeficient de fricció" és la relació de la força de fricció amb la força normal, que comprimeix dues superfícies oposades.
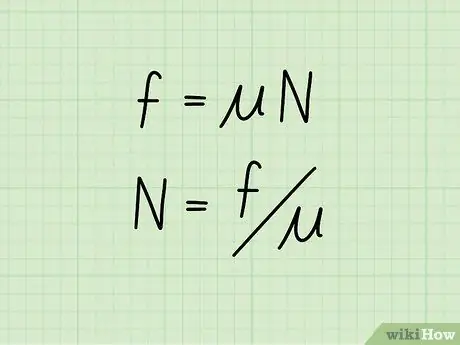
Pas 2. Configureu l'equació per aïllar la força normal
Si coneixeu el valor de la fricció cinètica d’un objecte, així com el seu coeficient de fricció, podeu calcular la força normal mitjançant la fórmula: N = f /
- Els dos costats de l'equació original es divideixen per ️, aïllant així la força normal per un costat mentre es calcula el coeficient de fregament i el fregament cinètic per l’altre.
- Exemple: trobeu la força normal d’un bloc si el coeficient de fregament és 0,4 i la magnitud del fregament cinètic és de 40 N.
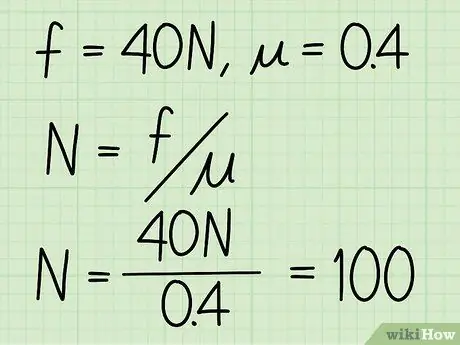
Pas 3. Divideix la fricció cinètica pel coeficient de fricció
Bàsicament, això és tot el que heu de fer per trobar la magnitud de la força normal.
Exemple: N = f / = 40/0, 4 = 100
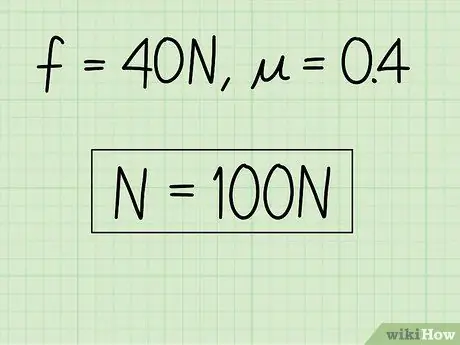
Pas 4. Escriviu les respostes
Si ho desitgeu, podeu comprovar la resposta connectant-la de nou a l'equació original per obtenir friccions cinètiques. Si no el voleu, heu resolt el problema.






