- Autora Jason Gerald [email protected].
- Public 2023-12-16 11:00.
- Última modificació 2025-01-23 12:09.
Per a la majoria de la gent, les fraccions són els primers càlculs complicats a trobar. El concepte de fraccions és força difícil i requereix que aprengueu condicions especials per fer-ho. Com que les fraccions tenen regles especials per a la suma, la resta, la multiplicació i la divisió, hi ha molta gent que està confosa al respecte. Tot i això, amb molta pràctica, tothom pot aprendre i completar càlculs relacionats amb les fraccions.
Pas
Mètode 1 de 5: entendre les fraccions
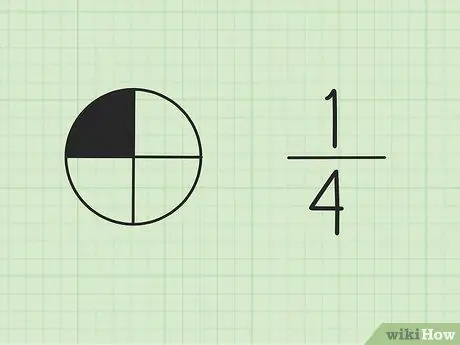
Pas 1. Comprendre que les fraccions formen part d’un tot
El número de la part superior s’anomena numerador i representa el nombre de parts del total. El número de la part inferior s’anomena denominador, que representa el nombre total de parts.
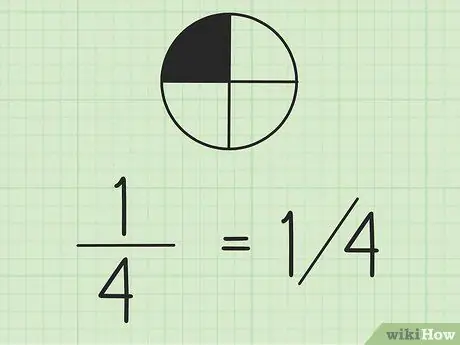
Pas 2. Tingueu en compte que podeu escriure fraccions amb barres inclinades
El número de l’esquerra és el numerador i el número de la dreta el denominador. Si esteu treballant amb fraccions a la mateixa línia, és una bona idea escriure el numerador a sobre del denominador.
Per exemple, si preneu una de les quatre llesques de pizza, en teniu. Si teniu 7/3 pizzes, vol dir que teniu dues pizzes senceres més 1 de 3 llesques de pizza
Mètode 2 de 5: Diferència entre fraccions mixtes i simples

Pas 1. Compreneu que els nombres mixtos consten de nombres enters i fraccions, per exemple 2 1/3 o 45 1/2
Normalment, heu de convertir nombres mixtos a una forma més senzilla per sumar, restar, multiplicar o dividir.

Pas 2. Canvieu el nombre mixt multiplicant el nombre sencer pel denominador de la fracció i afegint-lo pel numerador
Escriviu el resultat com a numerador, mentre que el denominador no canvia.
Per exemple, per convertir 2 1/3 en una fracció simple, multipliqueu 2 per 3 i, a continuació, afegiu-ne 1 i obteniu 7/3

Pas 3. Converteix fraccions simples en nombres mixtes dividint el numerador pel denominador
El resultat sencer de la divisió s’escriu com a enter i la resta de la divisió s’escriu com a numerador de la fracció. El denominador no canvia.
Per exemple, per convertir 7/3 a un nombre mixt, divideix 7 per 3 per obtenir 2 amb la resta de 1. Així que el nombre mixt és 2 1/3. Les fraccions simples només es poden convertir en nombres mixts si el numerador és superior al denominador
Mètode 3 de 5: sumar i restar fraccions
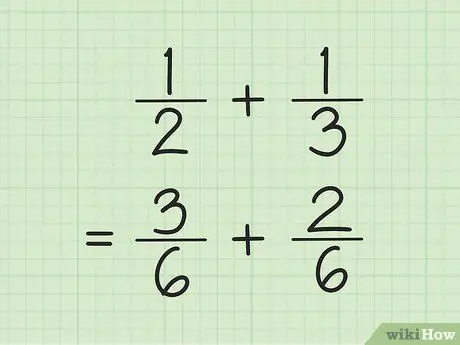
Pas 1. Cerqueu un denominador comú per sumar i restar fraccions
El truc, multiplica els números del denominador i multiplica cada numerador pel nombre utilitzat per trobar el denominador. De vegades, podeu trobar el MCM (mínim comú múltiple) per al denominador multiplicant els denominadors entre si.
Per exemple, per sumar i 1/3, primer cal trobar el MCM (mínim comú múltiple) dels dos denominadors multiplicant-se mútuament. Així, multipliqueu 2 i 3 per obtenir MCM 6. Multipliceu 1 per 3 per obtenir 3 com a nou numerador de la primera fracció. Multiplicar 1 per 2 per obtenir 2 com a nou numerador de la segona fracció. Les vostres noves fraccions són 3/6 i 2/6
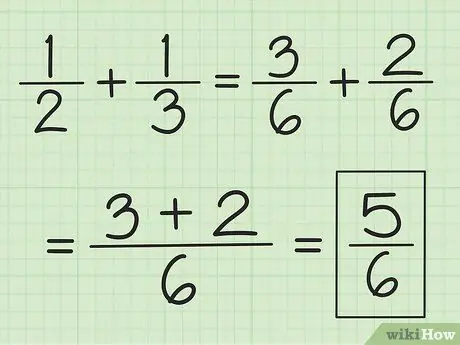
Pas 2. Afegiu els dos numeradors junts i no canvieu el denominador
Per exemple, 3/6 més 2/6 és 5/6 i 2/6 més 1/6 és 3/6
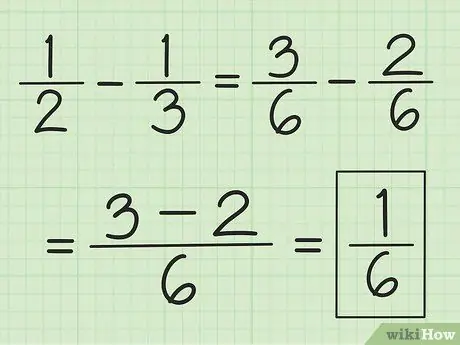
Pas 3. Utilitzeu una tècnica similar per a la resta
Cerqueu primer el MCM dels denominadors, però en lloc de sumar-los, resteu el nombre del primer numerador pel número del segon.
Per exemple, per restar 1/3 de 1/2, primer canvieu les fraccions a 3/6 i 2/6 i després resteu 3 per 2 per obtenir 1. Això resulta en 1/6
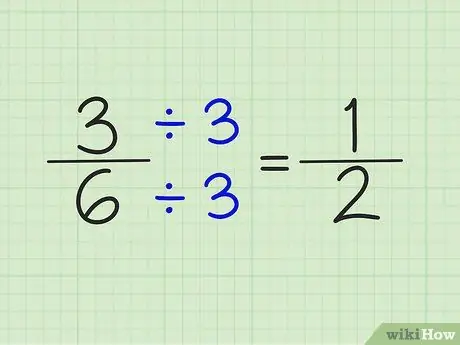
Pas 4. Simplifiqueu les fraccions dividint el numerador i el denominador pel mateix nombre
Per exemple, el número 5/6 no es pot simplificar. Tanmateix, 3/6 es pot simplificar dividint el numerador i el denominador pel nombre 3. El resultat és una fracció de 1/2

Pas 5. Converteix la fracció en un nombre mixt si el numerador és més gran que el denominador
Mètode 4 de 5: Multiplicar i dividir les fraccions
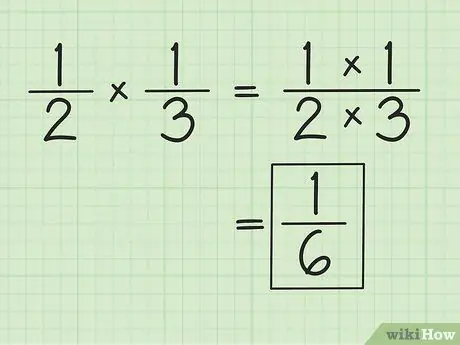
Pas 1. Multiplicar el numerador i el denominador per separat per multiplicar fraccions
Per exemple, en multiplicar i 1/3, el resultat és 1/6 (1 vegades 1 i 2 vegades 3). No cal que coincideixi amb els denominadors quan es multipliquen les fraccions. Simplifiqueu o modifiqueu els resultats obtinguts, si cal
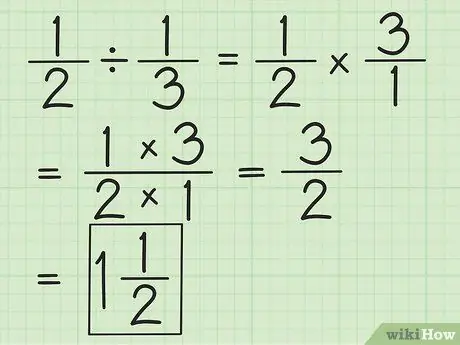
Pas 2. Divideix dues fraccions invertint la segona fracció i multiplicant les dues fraccions
Per exemple, si voleu dividir 1/2 per 1/3, primer inverteu la segona fracció a 3/1. Multiplicar per 3/1 i obtenir 3/2. Simplifiqueu les fraccions o converteu-les en nombres mixts, si és possible
Mètode 5 de 5: Treballar amb fraccions complexes
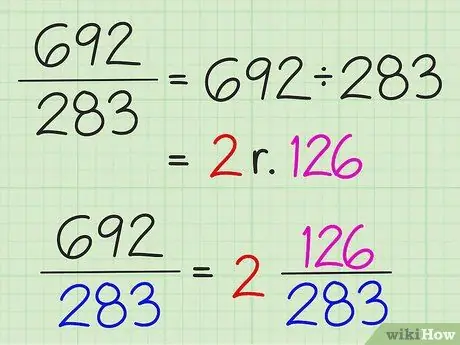
Pas 1. Treballeu totes les fraccions de la mateixa manera, encara que el problema sembli molt complicat
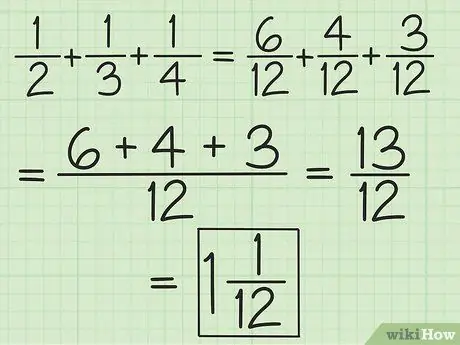
Pas 2. Relaciona els denominadors de totes les fraccions o treballa per parelles començant d’esquerra a dreta per sumar i restar més de dues fraccions
Per exemple, per sumar 1/2, 1/3 i 1/4, podeu canviar-los a 6/12, 4/12 i 3/12 per obtenir el 13/12, o podeu afegir 3/6 i 2 / 6 de manera que obtingueu 5/6 i, a continuació, afegiu 5/6 i 1/4 (igualeu els denominadors de manera que la segona fracció es converteixi en 3/12) per obtenir 13/12 (10/12 més 3/12). Converteix-lo en un nombre mixt, que és 1 1/12
Consells
- Recordeu que heu après força matemàtiques. Les matemàtiques són com un idioma que es pot pronunciar amb fluïdesa i que ara intenta aprendre a llegir-lo i a escriure-ho.
- Recordeu que sempre heu de simplificar el resultat final del vostre càlcul, tant si el vostre problema té la forma d’una fracció ordinària, com un nombre mixt o com una fracció complexa.






