- Autora Jason Gerald [email protected].
- Public 2023-12-16 11:00.
- Última modificació 2025-01-23 12:09.
Si ja ho enteneu, convertir fraccions ordinàries en decimals no és difícil. Per convertir fraccions comunes en decimals, podeu utilitzar divisions llargues, multiplicacions o fins i tot una calculadora si no voleu calcular-les a mà. Un cop hàgiu dominat el mètode, podreu convertir fàcilment les fraccions en decimals.
Pas
Mètode 1 de 4: amb divisió llarga
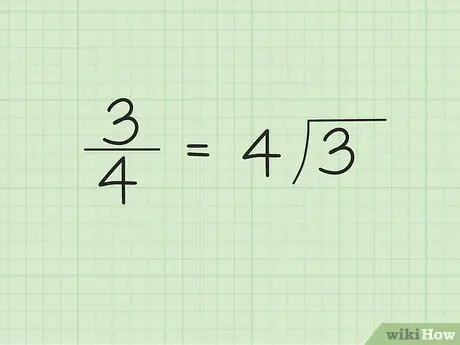
Pas 1. Escriviu el denominador fora / costat esquerre del símbol divisor i el numerador dins / costat dret del símbol divisor
Per exemple, suposem que volem convertir 3/4 en decimal. Escriviu "4" a l'exterior / costat esquerre del símbol divisor i "3" a l'interior / costat dret del símbol divisor. "4" és el nombre que divideix i "3" és el nombre que es divideix.

Pas 2. Escriviu "0", després un punt decimal (una coma), a sobre del símbol divisor
Com que és una fracció que compta, el resultat ha de ser inferior a un, de manera que aquest pas és molt important. Després d'això, escriviu el signe decimal, després "0", després del número "3" al costat dret del símbol divisor. Tot i que "3" és igual a "3, 0", el zero permet dividir "3, 0" per "4".

Pas 3. Calculeu la resposta mitjançant una divisió llarga
Amb la divisió llarga, de moment, el signe decimal es pot ignorar, de manera que només cal calcular 30 dividits per 4. A continuació s'explica com:
- En primer lloc, divideix 3, 0, que compta com a 30, per 4. El 4 a 30 més proper és 4 x 7 = 28, deixant 2. Per tant, escriu "7" després de "0", a sobre del divisor i "28" a " 3, 0”dins / costat dret del símbol divisor. Menors de 28 anys, escriviu "2", la resta de 30 menys 28.
- A continuació, escriviu "0" després de "3, 0" perquè es converteixi en "3, 00", que es pot considerar com a "300", a l'interior / costat dret del símbol divisor. Així, es pot reduir 0 a la dreta de "2" de manera que "20" sigui divisible per "4".
- "20" dividit per "4" és igual a "5". Per tant, escriviu "5" després de "0,7" a sobre del símbol divisor perquè es converteixi en "0,75".

Pas 4. Escriviu la resposta final
Per tant, "3" dividit per "4" equival a "0,75". Anota la resposta. Acabat.
Mètode 2 de 4: Fraccions que generen decimals repetitius
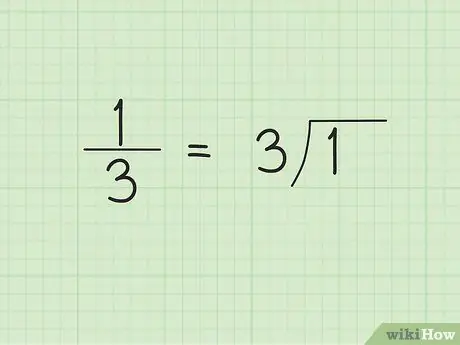
Pas 1. Fer divisió de divisió llarga
Quan comenceu la divisió de dígits llargs, és possible que no pugueu predir que el resultat serà un número decimal que es repeteix. Per exemple, suposem que volem convertir la fracció comuna 1/3 a forma decimal. Escriviu 3, o el denominador, a la part exterior / esquerra del símbol divisor i 1 a l’interior / dreta del símbol divisor.

Pas 2. Escriviu un 0 i un signe decimal a sobre del símbol divisor
Com que el resultat ha de ser inferior a 1, aquest pas prepara la resposta per escriure-la en forma decimal. El signe decimal també s'ha d'escriure a la dreta del número "1" situat al costat dret del símbol divisor.
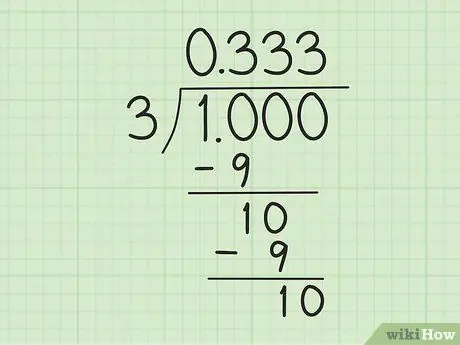
Pas 3. Comenceu a calcular la divisió de divisió llarga
Comenceu per convertir "1" en "1, 0", que compta com a "10", de manera que sigui divisible per "3". A continuació, realitzeu els passos següents:
- Dividiu 10 per 3. Utilitzeu 3 x 3 = 9 per fer la resta de 1. Per tant, escriviu 3 a la dreta del "0" sobre el símbol divisor i resteu 10 per 9 per obtenir la resta d'1.
- Escriviu un "0" a la dreta del número "1" (el restant de 10 menys 9 del pas anterior) a continuació per obtenir un altre "10". Quan es divideix de nou "10" per "3", es repeteix el mateix procés: escriviu "3" a la dreta del primer "3" per sobre del símbol divisor i resteu el nou "10" per "9".
- Continueu fins que es formi un patró. Saps que alguna cosa és estrany? Aquesta divisió pot continuar per sempre. 10 sempre és divisible per 3: sempre hi haurà un "1" a la part inferior i un nou "3" després del decimal a sobre del símbol divisor.
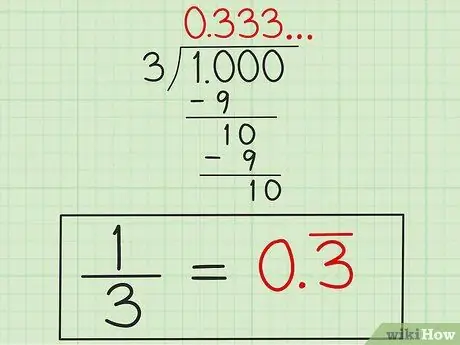
Pas 4. Escriviu la resposta
Després de saber que "3" es repetirà, escriviu la resposta com a "0, 3" amb una línia per sobre del número "3" (o "0, 33" amb una línia per sobre dels dos números "3") com a indicació que número "3" que es repeteix. Aquesta resposta té la forma decimal 1/3 perquè 1 dividit per 3 no acabarà per si sol.
Hi ha moltes fraccions que produeixen decimals que es repeteixen, com ara 2/9 ("0, 2" amb "2" que es repeteix), 5/6 ("0, 83" amb "3" que es repeteix) o 7/9 ("0, 7 "amb" 7 "continua repetint-se). Aquest patró sempre es produeix quan el denominador és múltiple de 3 i el numerador no pot ser divisible pel denominador
Mètode 3 de 4: Per multiplicació

Pas 1. Trobeu el nombre que es pot multiplicar pel denominador de la fracció per produir 10, 100, 1.000 o qualsevol nombre que sigui base 10
Aquesta pot ser una manera fàcil de convertir fraccions en decimals sense fer servir una divisió llarga ni una calculadora. En primer lloc, només cal trobar un nombre que es pugui multiplicar pel denominador de la fracció per obtenir 10, 100, 1.000, etc. Per fer-ho, primer divideix 10, després 100, després 1.000, i així successivament pel denominador fins obtenir un enter. Exemple:
- 3/5. 10/5 = 2.2 és un nombre enter. 2 es pot multiplicar per 5 per fer 10. Per tant, es poden utilitzar 2.
- 3/4. 10/4 = 2, 5. 2, 5 no és un nombre enter. 100/4 = 25. 25 és un nombre enter. 25 es pot multiplicar per 4 per fer-ne 100. Per tant, es poden utilitzar 25.
- 16/05. 16/10 = 0, 625, 100/16 = 6, 25, 1.000 / 16 = 62, 5, 10.000 / 16 = 625. 625 és el primer enter obtingut. 625 es poden multiplicar per 16 per obtenir 10.000. Per tant, es poden utilitzar 625.
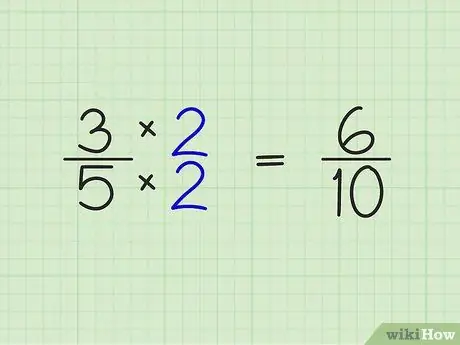
Pas 2. Multiplicar el numerador i el denominador de la fracció pel nombre sencer obtingut del pas anterior
Aquest pas és molt fàcil. Simplement multipliqueu els nombres per sobre i per sota de la fracció pel nombre sencer que heu obtingut al pas anterior. Exemple:
- 3/5 x 2/2 = 6/10
- 3/4 x 25/25 = 75/100
- 5/16 x 625/625 = 3,125 / 10000

Pas 3. Escriviu la resposta final
La resposta és que el numerador es marca amb un decimal segons el nombre de 0 del denominador. Només cal comptar quants 0 hi ha al denominador. Si només hi ha 1 0 al denominador, moveu el punt decimal a l'esquerra amb 1 dígit, etc. Exemple:
- 3/5 = 6/10 = 0, 6
- 3/4 = 75/100 = 0, 75
- 5/16 = 3.125/10.000 = 0, 3125
Mètode 4 de 4: amb calculadora

Pas 1. Divideix el numerador pel denominador
Aquest mètode és molt fàcil. Només cal que utilitzeu una calculadora per dividir el numerador, el número situat a la part superior de la fracció, pel denominador, el nombre a la part inferior de la fracció. Per exemple, suposem que voleu convertir 3/4 en decimal. Simplement premeu "3", després el símbol de divisió ("÷ '"), després "4" i, finalment, el símbol igual ("=").

Pas 2. Escriviu les respostes que obtingueu
La resposta és 0,75, per tant, la forma decimal de la fracció comuna 3/4 és 0,75.
Consells
- Per comprovar si la resposta és correcta, multipliqueu la resposta pel denominador de la fracció. Si la vostra resposta és correcta, el producte de la multiplicació és el numerador de la fracció.
- Algunes fraccions es poden convertir en decimals creant fraccions comparables els denominadors de les quals són la base 10 (10, 100, 1.000, etc.). A continuació, utilitzeu valors de lloc per escriure la forma decimal correcta.






