- Autora Jason Gerald [email protected].
- Public 2023-12-16 11:00.
- Última modificació 2025-01-23 12:10.
Comptar fraccions és una de les habilitats matemàtiques més útils per desenvolupar. Abans de fer càlculs fraccionaris, apreneu a identificar parts i tipus de fraccions. Després, podeu afegir-los o restar-los. Per obtenir càlculs més complexos, apreneu a multiplicar i dividir fraccions. Normalment, també haureu de simplificar o reduir les fraccions.
Pas
Mètode 1 de 4: reconeixement de fraccions

Pas 1. Trobeu la fracció
Les fraccions s’escriuen com un número per sobre de la línia divisòria i un altre número per sota de la línia.
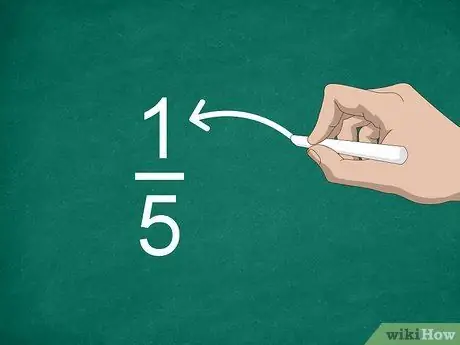
Pas 2. Identifiqueu el numerador
El número situat a sobre de la línia s’anomena numerador i mostra quantes parts hi ha a la fracció.
Per exemple, a la fracció 1/5, "1" és el numerador
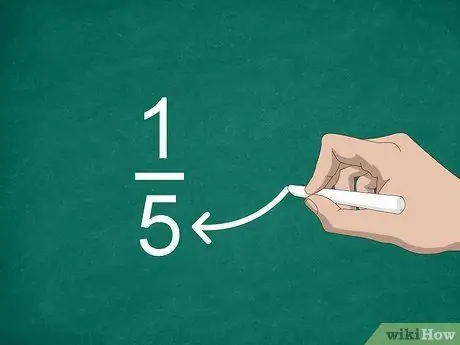
Pas 3. Cerqueu el denominador
El nombre situat sota la línia s’anomena denominador. Aquest valor indica el nombre de parts que "construeixen" un nombre enter.
Per exemple, a la fracció 1/5, "5" és el denominador, de manera que hi ha cinc parts a la fracció

Pas 4. Determineu si les fraccions són fraccions raonables o fraccions incorrectes
Si el numerador és més petit que el denominador, la fracció és una fracció natural. En fraccions impròpies, el numerador és més gran que el denominador.
- Per exemple, 3/4 és una fracció raonable i 5/3 és una fracció impròpia.
- Si teniu un nombre enter que inclou una fracció, el nombre es coneix com a nombre mixt. Per exemple, 1 1/2 és un nombre mixt.
Mètode 2 de 4: sumar o restar fraccions

Pas 1. Identifiqueu fraccions amb el mateix denominador
Si heu de sumar o restar fraccions, cada fracció ha de tenir el mateix denominador abans de realitzar el càlcul. Observeu el denominador de cada fracció per assegurar-vos que totes són iguals (similars).
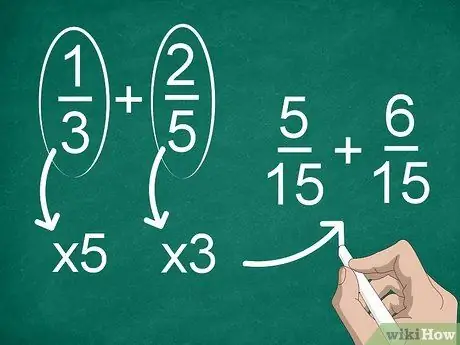
Pas 2. Trobeu un denominador comú si cada fracció té un denominador diferent
Si els denominadors no són els mateixos, haureu de canviar les fraccions per tenir el mateix denominador. Per trobar un denominador comú, multiplica cada fracció pel denominador de l’altra.
Per exemple, per trobar un denominador comú a 1/3 + 2/5, multipliqueu "1" i "3" per "5", després multipliqueu "2" i "5" per "3". Ara teniu l’addició de 15/05 + 15/06. Després d'això, podeu calcular les fraccions
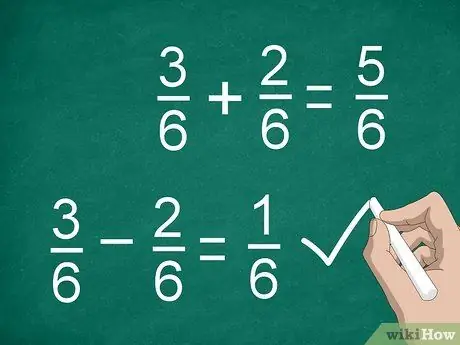
Pas 3. Sumeu o resteu els numeradors per calcular fraccions
Un cop heu trobat un denominador comú i heu multiplicat els numeradors (si cal), esteu a punt per sumar o restar. Sumeu o resteu els numeradors i col·loqueu el resultat per sobre de la línia divisòria. Escriviu el denominador comú sota la línia.
- Per exemple, 3/6 - 2/6 = 1/6.
- No sumeu ni resteu els denominadors.
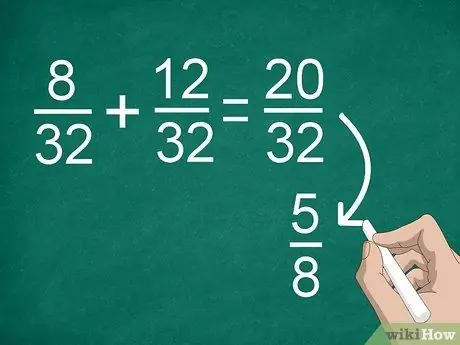
Pas 4. Simplifiqueu els resultats si cal
Si anteriorment calia trobar un denominador comú, és possible que obtingueu una fracció gran que podeu simplificar. Per exemple, si afegiu 8/32 +12/32, obtindreu el resultat "20/32". Aquesta fracció es pot simplificar a "5/8".
Mètode 3 de 4: Multiplicar i simplificar les fraccions
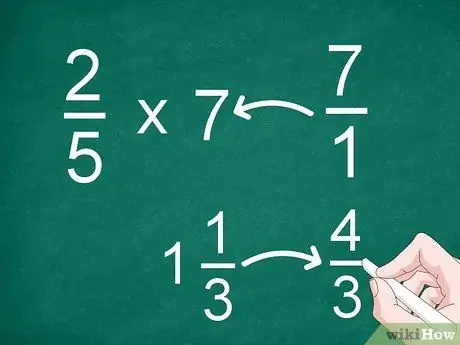
Pas 1. Converteix fraccions mixtes o enters en fraccions inadequades
Per facilitar la multiplicació, heu de convertir cada número en una fracció raonable o inadequada. Si teniu nombres enters o nombres mixts que cal multiplicar, primer convertiu-los en una fracció comuna (natural o impròpia).
- Per exemple, per multiplicar 2/5 per 7, converteix "7" en fracció. Després d'això, podeu multiplicar 2/5 per 7/1.
- Si teniu un nombre mixt com 1 1/3, converteix-lo en una fracció incorrecta ("4/3") abans de multiplicar-lo.
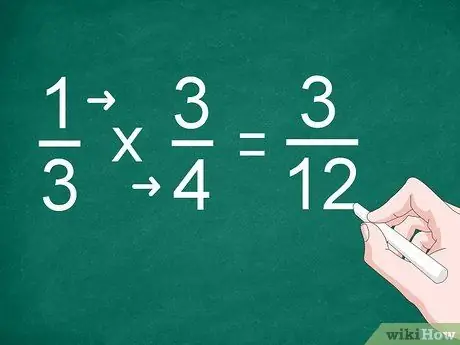
Pas 2. Multiplicar cada numerador i denominador
En lloc de fer una suma, multipliqueu el numerador i escriviu el resultat per sobre de la línia divisòria. També heu de multiplicar els denominadors i escriure el resultat a sota de la línia.
Per exemple, per multiplicar 1/3 per 3/4, multiplica "1" per "3" per obtenir el numerador. Multipliqueu "3" per "4" per obtenir el denominador. La resposta a la multiplicació és "3/12"

Pas 3. Simplifiqueu els resultats
Normalment, haureu de reduir el resultat a una forma més senzilla, sobretot si inicialment teniu fraccions no naturals. Trobeu el màxim factor comú i utilitzeu-lo per simplificar el numerador i el denominador.
Per exemple, per a la fracció 3/12, el màxim factor comú entre "3" i "12" és "3". Dividiu cada element de la fracció per "3" fins obtenir la fracció "1/4"
Mètode 4 de 4: divideix les fraccions
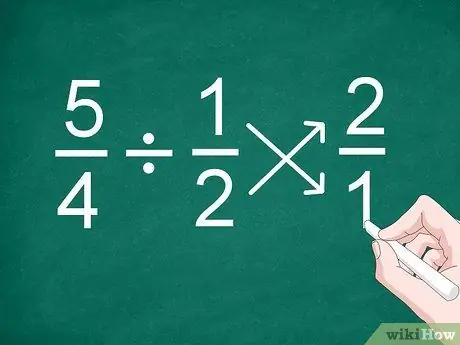
Pas 1. Invertiu la posició de la segona fracció
La forma més senzilla de dividir fraccions, fins i tot fraccions amb diferents denominadors, és invertir la posició de la segona fracció abans de calcular el resultat.
Per exemple, per al problema 5/4 1/2, inverteix la posició de la fracció "1/2" per convertir-la en "2/1"
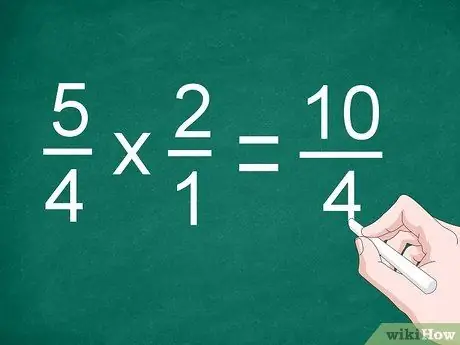
Pas 2. Multiplicar el numerador i el denominador
Multiplicar fraccions directament per multiplicar els numeradors. Escriviu el resultat per sobre de la línia divisòria i multipliqueu el denominador. Anoteu el producte dels denominadors a sota de la línia.
Per a l'exemple anterior, multipliqueu 5/4 per 2/1 per obtenir "10/4"
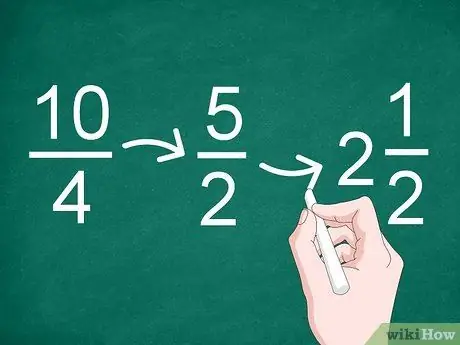
Pas 3. Simplifiqueu els resultats si cal
Si el resultat de la divisió és una fracció impròpia o es pot reduir, simplifiqueu la fracció. Utilitzeu el màxim factor comú per reduir la fracció.
- Per exemple, el màxim factor comú de la fracció 10/4 és "2", de manera que el resultat de la simplificació es converteix en "5/2" (10 dividit per 2 i 4 dividit per 2).
- Com que el resultat de la simplificació és una fracció impròpia, podeu convertir-la en un enter i una fracció (un nombre mixt). Per tant, 5/2 es pot canviar a "2".
Consells
- Si esteu treballant amb fraccions complexes, haureu de fer alguns passos addicionals per simplificar la fracció. Tot i això, aquesta simplificació és una part obligatòria del procés de càlcul.
- Escriviu sempre les fraccions ordenadament per reduir el risc d’errors de càlcul.






