- Autora Jason Gerald [email protected].
- Public 2024-01-19 22:11.
- Última modificació 2025-01-23 12:09.
Les matemàtiques són dures. És fàcil oblidar fins i tot els conceptes bàsics quan s’intenta recordar els diferents principis i mètodes diferents. Aquí hi ha dues maneres noves de simplificar les fraccions.
Pas
Mètode 1 de 4: utilitzar el màxim factor comú

Pas 1. Escriviu els factors del numerador i del denominador
Els factors són nombres que podeu multiplicar per obtenir un altre nombre. Per exemple, 3 i 4 són factors de 12 perquè podeu multiplicar-los junts per obtenir 12. Per escriure els factors d’un nombre, només cal que anoteu tots els números que es puguin multiplicar per obtenir aquest nombre i siguin divisibles. pels factors.
-
Escriviu els factors del nombre del més petit al més gran, sense oblidar d’incloure el factor 1. Per exemple, aquí s’escriu el numerador i el denominador de la fracció 24/32:
- 24: 1, 2, 3, 4, 6, 8, 12, 24.
- 32: 1, 2, 4, 8, 16, 32.

Pas 2. Trobeu el màxim comú factor (MCD) del numerador i el denominador
El MCD és el nombre més gran que pot dividir uniformement dos o més nombres. Després d’haver anotat tots els factors del nombre, tot el que heu de fer és trobar el nombre més gran que sigui el mateix a les dues llistes de factors.
-
24: 1, 2, 3, 4, 6,
Pas 8., 12, 24.
-
32: 1, 2, 4,
Pas 8., 16, 32.
-
El MCD de 24 i 32 és 8 perquè 8 és el nombre més gran que pot dividir uniformement 24 i 32.

Pas 3. Divideix el numerador i la fracció pel MCD
Ara que teniu el MCD, tot el que heu de fer és dividir el numerador i el denominador per aquest nombre per simplificar la vostra fracció a la forma més senzilla. A continuació s’explica com fer-ho:
- 24/8 = 3
- 32/8 = 4
- La fracció simple és 3/4.

Pas 4. Comproveu el vostre treball
Si voleu assegurar-vos que heu simplificat la fracció correctament, només heu de multiplicar el nou numerador i denominador pel seu PIB per recuperar la fracció original. A continuació s’explica com fer-ho:
- 3 * 8 = 24
- 4 * 8 = 32
-
Heu tornat a la seva forma original, que és 24/32.
També podeu comprovar la fracció per assegurar-vos que no es pugui simplificar més. Com que 3 és un nombre primer, només es pot dividir entre 1 i ell mateix, i quatre no és divisible per 3, de manera que la fracció no es pot simplificar més
Mètode 2 de 4: Seguiu dividint per xifres petites

Pas 1. Trieu un nombre petit
Amb aquest mètode, només haureu de triar un nombre petit, com ara 2, 3, 4, 5 o 7, per començar. Mireu les fraccions per assegurar-vos que cada part sigui divisible pel nombre que hàgiu triat. Per exemple, si teniu una fracció 24/108, no trieu 5 perquè no són divisibles per 5. Tanmateix, si teniu una fracció 25/60, 5 és el número correcte que cal utilitzar.
Per a la fracció 24/32, 2 és un bon nombre. Com que tots dos números són nombres parells, són divisibles per 2

Pas 2. Divideix el numerador i el denominador de la fracció pel nombre
La nova fracció consistirà en un nou numerador i denominador, que obtindreu després de dividir la part superior i inferior de la fracció 24/32 per 2. A continuació us expliquem com fer-ho:
- 24/2 = 12
- 32/2 = 16
- La vostra nova fracció és el 16/12.
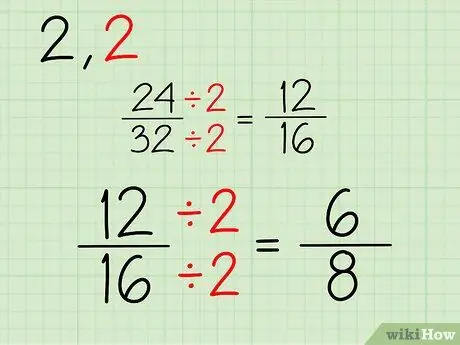
Pas 3. Repetiu
Continueu aquest procés. Com que tots dos números són nombres parells, podeu continuar dividint per 2. Si un o tots dos dels numeradors i denominadors són nombres senars, podeu provar de dividir per un altre nombre. Aquí teniu el procés per simplificar la fracció 12/16:
- 12/2 = 6
- 16/2 = 8
- La vostra fracció nova és de 6/8.

Pas 4. Seguiu dividint el número fins que deixi de ser divisible
El nou numerador i denominador també són nombres parells, de manera que podeu continuar dividint per 2. A continuació us expliquem com fer-ho:
- 6/2 = 3
- 8/2 = 4
- La vostra nova fracció és 3/4.

Pas 5. Assegureu-vos que la fracció no es pugui simplificar més
A la fracció 3/4, 3 és un nombre primer, de manera que els factors són només 1 i ell mateix, i 4 no és divisible per 3, de manera que la fracció no es pot simplificar més. Si el numerador o el denominador de la fracció ja no es pot dividir pel nombre que heu seleccionat, és possible que pugueu dividir-lo per un altre número.
Per exemple, si teniu la fracció 10/40 i dividiu el numerador i el denominador per 5, el resultat és 2/8. No podeu continuar dividint el numerador i la fracció per 5, però podeu dividir-los per 2, de manera que el resultat final és 1/4

Pas 6. Comproveu el vostre treball
Torneu a multiplicar 3/4 per 2/2 tres vegades, per assegurar-vos que obteniu la fracció inicial, que és 24/32. A continuació s’explica com fer-ho:
- 3/4 * 2/2 = 6/8
- 6/8 * 2/2 = 12/16
- 12/16 * 2/2 = 24/32.
- Fixeu-vos que esteu dividint 24/32 per 2 * 2 * 2, que és el mateix que dividir per 8, el MCD més gran de 24 i 32.
Mètode 3 de 4: escriure els factors

Pas 1. Escriviu la vostra fracció
Deixeu un espai ampli a la part dreta del paper; el necessitareu per anotar els factors.

Pas 2. Escriviu els factors del numerador i del denominador
Sols els factors dels dos. La forma més senzilla és que els factors s’escriuen l’un sobre l’altre. Comenceu pel número 1 i escriviu els factors.
-
Per exemple, si la vostra fracció és 24/60, comenceu per 24.
Anoteu: 24 - 1, 2, 3, 4, 6, 8, 12, 24
-
Després, el número 60.
Anoteu: 60 - 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

Pas 3. Trobar i dividir pel màxim factor comú
Aquest terme es pot escriure en format PDF al vostre llibre imprès. Quin és el nombre més gran que pot dividir el numerador i el denominador? Sigui quin sigui el nombre, dividiu els dos números per aquest nombre.
Per al nostre exemple, el nombre més gran que és factor d’ambdós nombres és 12. Per tant, dividim 24 per 12 i 60 per 12, donant-nos 2/5, la nostra fracció simple
Mètode 4 de 4: utilitzar un arbre de factors primers

Pas 1. Trobeu els factors primers del numerador i del denominador
Un nombre primer és un nombre que no es pot dividir per cap altre nombre (que no sigui ell mateix i 1, és clar). 2, 3, 5, 7 i 11 són exemples de nombres primers.
- Comenceu pel numerador. A partir del 24, divideix-lo en 2 i 12. Com que el 2 ja és un nombre primer, ja no cal dividir-lo. A continuació, divideix 12 en 2 nombres: 2 i 6. 2 són nombres primers - fantàstic! Ara divideix 6 en 2 nombres: 2 i 3. Ara tens 2, 2, 2 i 3 com a nombres primers.
- Ara treballeu en el denominador. A partir de 60, divideix el teu arbre en 2 i 30. 30 i després divideix-ho en 2 i 15. A continuació, divideix 15 en 3 i 5, tots dos números primers. Ara teniu 2, 2, 3 i 5 com a nombres primers.
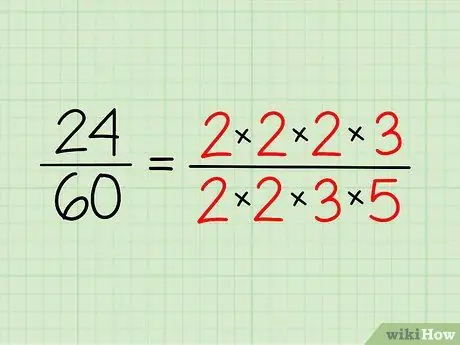
Pas 2. Escriviu la factorització primera de cada nombre
Escriviu els nombres primers que tingueu per a cada número i escriviu-los en forma de multiplicació. No cal que el multipliqueu; només és una manera de facilitar la visió.
- Per tant, per a 24, teniu 2 x 2 x 2 x 3 = 24.
- Per a 60, teniu 2 x 2 x 3 x 5 = 60

Pas 3. Elimineu els mateixos factors
Es pot descartar qualsevol número que formi part dels dos números. En aquest exemple, els factors iguals són un parell de 2 i un 3. Adéu!
- La resta són 2 i 5 - o 2/5! La mateixa resposta que vam obtenir és la següent.
- Si el numerador i el denominador de la fracció són nombres parells, no dividiu només per dos. Continueu fent la divisió fins que el número que obtingueu no es pugui tornar a dividir.






