- Autora Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 11:00.
- Última modificació 2025-01-23 12:10.
El sistema numèric decimal (base deu) té deu valors possibles (0, 1, 2, 3, 4, 5, 6, 7, 8 o 9) per a cada posició numèrica. En canvi, el sistema numèric binari (base dos) només té dos valors possibles representats per 0 i 1 per a cada posició numèrica. Atès que el sistema de números binaris és el llenguatge intern dels ordinadors electrònics, els programadors informàtics seriosos saben convertir del sistema decimal a binari. Seguiu aquests senzills passos i també com dominar aquesta conversió.
Pas
Mètode 1 de 2: Divisió curta per dos amb resta

Pas 1. Determineu el problema
Per a aquest exemple, convertim el nombre decimal 15610 ser un número binari. Escriviu el número decimal com a número a dividir en el símbol de divisió invertida. Escriviu la base del sistema numèric de destinació (en aquest exemple “2” per a binari) com a divisor fora de corba del símbol de divisió.
- Aquest mètode és molt més fàcil d’entendre quan es dibuixa en paper i molt més fàcil per als principiants, perquè només es divideix per dos.
- Per evitar confusions abans i després de la conversió, escriviu el número base del sistema numèric que esteu calculant com a subíndex (minúscules escrites amb lletres normals com a signe distintiu) per a cada número. En aquest exemple, el nombre decimal tindrà un subíndex de 10 i el número binari tindrà un subíndex de 2.

Pas 2. Feu la divisió
Escriviu la resposta sencera (quocient) sota el símbol de divisió llarga i escriviu la resta (0 o 1) a la dreta del número dividit.
Com que dividim per dos, quan el nombre que es divideix és un nombre parell, la resta és 0, i quan el nombre que es divideix és un nombre senar, el restant és 1

Pas 3. Continueu dividint fins que arribi a zero
Continueu baixant, dividint cada quocient nou per dos i escrivint la resta a la dreta de cada número dividit. Atureu-vos quan el quocient sigui zero.

Pas 4. Escriviu el nou número binari
A partir del nombre restant més baix, llegiu l'ordre de la resta en ordre ascendent fins a la part superior. En aquest exemple, hauríeu d'obtenir el resultat 10011100. Aquest és l'equivalent binari del nombre decimal 156. O, si s'escriu amb el seu índex de base numèrica: 15610 = 100111002.
Aquest mètode es pot modificar per convertir de base decimal a qualsevol base numèrica. El divisor és 2 perquè la base del sistema numèric de destinació és la base 2 (binària). Si la base del sistema numèric de destinació és una altra base, substituïu el número base 2 d’aquest mètode pel número base adequat. Per exemple, si la base de destinació és la base 9, substituïu el número base 2 per 9. El resultat final serà directament en la forma del número base de destinació
Mètode 2 de 2: Potència derivada de dos i resta

Pas 1. Comenceu creant una taula
Escriviu les potències dels dos números base a la "base de la taula 2" de dreta a esquerra. Comenceu a les 20, escriviu-lo com a "1". Augmenteu el rang en 1 per a cada rang. Completeu la taula fins que obtingueu un nombre més proper al número del sistema de nombres decimals que esteu calculant. Per a aquest exemple, convertim el nombre decimal 15610 ser un número binari.

Pas 2. Cerqueu el nombre amb la potència més gran del número base 2
A la taula, trieu el nombre més gran que sigui igual o inferior al nombre que voleu convertir. El número 128 és el nombre amb la potència més gran del número base 2 i també és inferior a 156, així que escriviu un número "1" sota aquest quadre de la taula, on el nombre més gran de la taula es troba a l'esquerra (vegeu la taula a la imatge superior). A continuació, resteu 128 del número inicial i obtindreu: 156 - 128 = 28.
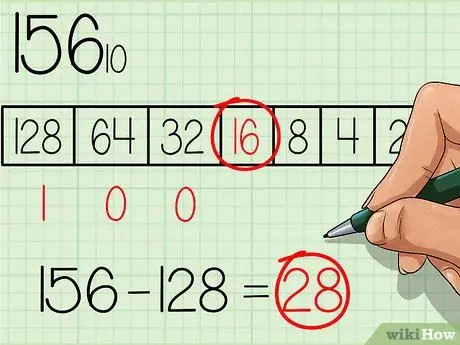
Pas 3. Passeu a la següent potència més petita de la taula
Amb el número nou (28), continueu per la taula d’esquerra a dreta mentre comproveu si els números són iguals o inferiors al número nou. El número 64 no és inferior a 28, així que escriviu el número “0” a sota del quadre número 64. Continueu fins que trobeu un número igual o inferior a 28.
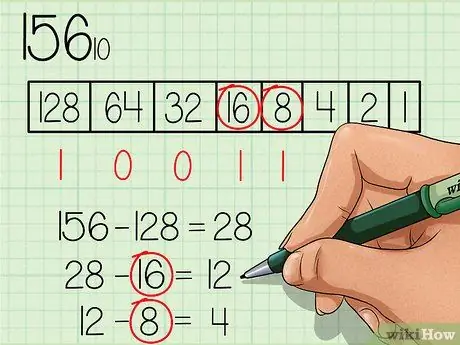
Pas 4. Resteu de forma contínua tots els números que siguin iguals o inferiors al número nou i marqueu el número "1" a sota del quadre per al número adequat
El número 16 és inferior a 28, així que escriviu el número "1" a la casella 16 i resteu 16 de 28, de manera que obtingueu un número nou 12. El número 8 és inferior a 12, així que escriviu el número "1" a sota el quadre número 8 i restar 8 de 12 per obtenir el nou número 4.

Pas 5. Continueu fins que arribeu al final de la taula
Recordeu marcar un "1" a sota de cada casella per als números que siguin iguals o inferiors al número nou i un "0" a cada casella per als números que siguin superiors al número nou.
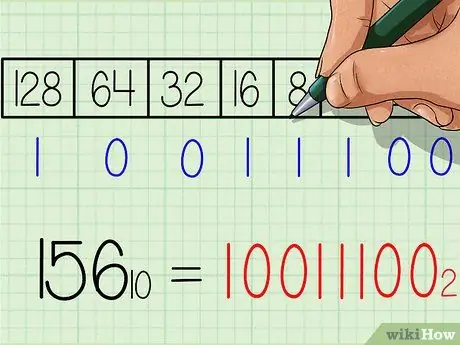
Pas 6. Escriviu la resposta del número binari
El número serà exactament el mateix d'esquerra a dreta que la fila de números "1" i "0" a la part inferior de la taula. Haureu d'obtenir el resultat 10011100. Aquest és l'equivalent binari del nombre decimal 156. O quan s'escriu amb un subíndex: 15610 = 100111002.
Repetir aquest mètode us pot ajudar a recordar els poders de la base dos, de manera que podeu ometre el pas 1
Consells
- El programa Calculadora integrat al sistema operatiu us pot fer aquesta conversió, però, com a programador, és millor començar comprenent bé el funcionament de les conversions. Les opcions de conversió del programa Calculadora es poden fer visibles obrint el menú "Veure" i seleccionant "Programador" (per a Windows 7 i 8).
- La conversió en sentit contrari, és a dir, del sistema de números binari a decimal, sol ser més fàcil d’aprendre primer.
- Sovint practiqueu la conversió de nombres decimals a binaris per ser més experts.






