- Autora Jason Gerald [email protected].
- Public 2024-01-15 08:11.
- Última modificació 2025-01-23 12:10.
A les estadístiques, el mode és el número que apareix més sovint en un conjunt de números o dades. les dades en si mateixes no sempre tenen només un mode, poden ser dues o més (per tant, s’anomenen bimodals o multimodals). En altres paraules, tots els números que es produeixen amb més freqüència en una dada es poden anomenar mode. Per esbrinar com trobar el mode, seguiu els passos següents.
Pas
Mètode 1 de 2: trobar el mode de dades

Pas 1. Escriviu els números a les dades
El mode normalment es pren a partir de dades estadístiques o d’una llista de nombres. Per tant, necessiteu dades per trobar el mode. Es recomana enregistrar o escriure les dades primer, perquè trobar el mode només veient-lo i analitzant-lo és molt difícil, tret que les dades siguin molt poques. Si utilitzeu paper, llapis o bolígraf, només cal que anoteu les dades per ordenar-les després. Si teniu un ordinador, podeu utilitzar un programa de full de càlcul per ordenar-los automàticament més endavant.
El procés de trobar el mode de dades és més fàcil d’entendre si el seguim a partir d’un problema d’exemple. Per ara, fem servir aquestes dades de mostra: {18, 21, 11, 21, 15, 19, 17, 21, 17}. En els propers passos descobrirem el mode.

Pas 2. Ordeneu els números del més petit al més gran
En realitat, no es pot ordenar les dades. Però aquest pas realment us ajudarà a trobar el mode, ja que els mateixos números estaran l'un al costat de l'altre, cosa que facilitarà el càlcul. Si la mida de les vostres dades és molt gran, s'ha de fer aquest pas per reduir la taxa d'ocurrència propensa a errors.
- Si feu servir paper, llapis o bolígraf, torneu a escriure les dades que heu escrit anteriorment per ordre. Comenceu per trobar el nombre més petit de les dades. Si el trobeu, escriviu-lo en una nova línia i, a continuació, ratlleu el número de la llista de dades anterior. Cerqueu el número més petit següent i feu el mateix fins que hagueu ordenat tots els números.
- Si utilitzeu un programa de full de càlcul a l’ordinador, podeu ordenar la llista de números amb només uns clics.
-
En el nostre exemple anterior, les dades ordenades són {11, 15, 17, 17, 18, 19, 21, 21, 21}.

Pas 3. Compteu el nombre de vegades que apareix un número
Per a dades petites, només podeu mirar les dades que s’han ordenat i, a continuació, cercar quin número hi és més visible. Si les vostres dades són més grans, heu de calcular-les una per una per evitar errors.
- Si feu servir paper, llapis o bolígraf, per evitar errors de càlcul, observeu quantes vegades apareix cada número. Si utilitzeu un full de càlcul en un ordinador, també podeu enregistrar-lo en una altra columna o, si ho sabeu, podeu utilitzar les fórmules proporcionades al programa.
- En el problema d’exemple, és a dir ({11, 15, 17, 17, 18, 19, 21, 21, 21}), el número 11 apareix una vegada, el 15 es produeix una vegada, el 17 es produeix dues vegades, el 18 es produeix una vegada, el 19 es produeix una vegada, i 21 apareix tres vegades. A partir d’aquí, queda clar que 21 és el nombre que apareix amb més freqüència.

Pas 4. El número que apareix amb més freqüència és el mode de les dades
Després de constatar quantes vegades apareix cadascun dels mateixos números, ja ho hauríeu de saber quin número apareix més, que significa el mode de dades. Recorda que és possible que una dada tingui més d’un mode. Si una dada té dos modes, les dades es poden anomenar bimodals, mentre que si tenen tres modes, s’anomenen trimodals, etc.
- A l'exemple del problema, el mode és 21 perquè apareix amb més freqüència.
- Si hi ha un altre número que també apareix tres vegades, llavors el 21 és aquest mode.

Pas 5. Diferencieu el mode de les dades per la seva mitjana (mitjana) i mitja
Els tres conceptes estadístics se solen discutir en una discussió. Com que tenen noms similars i, de vegades, tenen el mateix valor, a moltes persones els costa distingir-los. Tanmateix, tot i que les dades poden tenir el mateix mode, mitjà o mitjà, tingueu en compte que són diferents i es mantenen sols. Llegiu l’explicació següent.
-
La mitjana que significa la mitjana és la suma dels valors de les dades dividida pel nombre de dades. Per exemple, al problema d'exemple ({11, 15, 17, 17, 18, 19, 21, 21, 21}), les dades totals són 11 + 15 + 17 + 17 + 18 + 19 + 21 + 21 + 21 = 160. I com que hi ha 9 valors a les dades, llavors 160/9 = 17.78.

Cerqueu el mode d'un conjunt de números Pas 5 Bullet1 -
La mediana és el valor mitjà després d'ordenar les dades i separa els valors petit i gran de les dades. En el problema d’exemple ({11, 15, 17, 17, 18, 19, 21, 21, 21}), la mediana és
Pas 18. perquè el nombre es troba al centre i hi ha quatre números superiors i quatre números inferiors a 18 a les dades. Si les dades són un nombre parell, la mediana s’obté calculant la suma dels dos nombres al mig i dividint-la per dos.

Cerqueu el mode d'un conjunt de números Pas 5 Bullet2
Mètode 2 de 2: trobar el mode en un problema especial

Pas 1. Les dades no tenen mode si tots els números de les dades tenen el mateix nombre d’ocurrències
Per exemple, si tots els números només apareixen una vegada, les dades sense mode perquè cap dels dos números apareix amb més freqüència que l’altre. El mateix passa si tots els números apareixen dues vegades o més.
Si canviem les dades del problema d’exemple anterior a {11, 15, 17, 18, 19, 21}, el que significa que tots els números apareixen una vegada, les dades no tenen mode, així com si les dades es canvien a {11, 11, 15, 15, 17, 17, 18, 18, 19, 19, 21, 21}

Pas 2. Totes les dades no numèriques es poden cercar pel seu mode, com ara les dades numèriques
Normalment, les dades estan presents en forma quantitativa o numèrica, de manera que es poden processar mitjançant molts mètodes. Tanmateix, de vegades hi ha coses que no tenen forma de nombres. Tanmateix, aquest mode de dades encara es pot cercar simplement cercant les dades (que poden ser en forma d’enunciats) que es produeixen amb més freqüència. Però no podeu trobar la mitjana ni la mitjana de les dades no numèriques.
- Per exemple, suposem que feu una enquesta biològica, que consisteix a esbrinar quines espècies d’arbres creixen a la vostra zona. Les dades que obteniu són {Fire, Mango, Spruce, Palm, Spruce, Fir, Mango, Mango, Palm, Fir}. Aquestes dades s’anomenen dades nominals perquè cada valor de les dades es distingeix per un nom. Per a aquest exemple, el mode és avet perquè apareix més sovint (cinc vegades).
- Si mireu l’exemple, no podeu calcular la mitjana ni la mitjana.
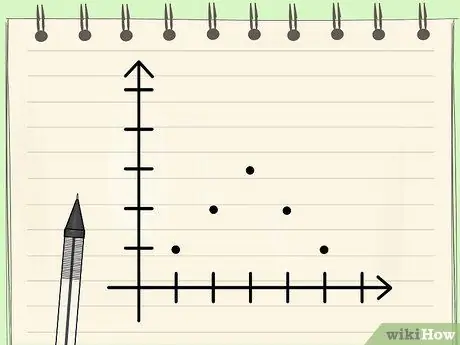
Pas 3. Sabeu que per a una distribució simètrica de dades unimodals, el mode, la mediana i la mitjana de les dades seran les mateixes
Com s’ha esmentat anteriorment, hi haurà moments en què la mitjana, la mediana i el mode d’un conjunt de dades siguin els mateixos. Una de les condicions és si una dada té una distribució de valors estrictament simètrica (que si es dibuixa en forma gràfica formarà una corba gaussiana en forma de campana). Com que la distribució és simètrica, el mode de dades com aquest és automàticament les dades que es troben al centre, perquè han de ser les dades que apareixen amb més freqüència i perquè és el valor mitjà, vol dir que el nombre també és la mediana. I si feu les matemàtiques, la mitjana donarà el mateix nombre.
- Per exemple, a partir de les dades {1, 2, 2, 3, 3, 3, 4, 4, 5}, si dibuixeu el gràfic, obtindreu un gràfic d’una paràbola. El mode de dades és 3 perquè apareix més sovint, la mitjana és de 3 perquè el número està al mig i la mitjana és 1 + 2 + 2 + 3 + 3 + 3 + 4 + 4 + 5 = 27/9 = 3.
- Casos com aquest tenen excepcions, és a dir, quan aquestes dades simètriques tenen més d’un mode. Si aquest és el cas, perquè la mitjana i la mediana no poden ser més d’un valor, el mode no serà el mateix que la mitjana i la mediana.
Consells
- Les dades poden tenir més d’un mode
- Si el nombre d’ocurrències de tots els números en una dada és el mateix, el mode de dades no existeix.






