- Autora Jason Gerald [email protected].
- Public 2024-01-19 22:11.
- Última modificació 2025-01-23 12:10.
La resta és simplement restar un número a un altre. És fàcil restar un nombre enter d’un altre, però la resta pot ser complicada si resteu fraccions o decimals. Un cop hàgiu entès la resta, podreu utilitzar conceptes matemàtics més complexos i afegir, multiplicar i dividir nombres amb més facilitat.
Pas
Mètode 1 de 6: restar grans nombres sencers per préstec

Pas 1. Escriviu un gran nombre
Per exemple, voleu resoldre 32 - 17. Escriviu primer 32.

Pas 2. Escriviu el nombre més petit just a sota
Assegureu-vos que col·loqueu els valors de desenes i un a les columnes correctes, de manera que 3 de 32 estigui directament per sobre de 1 de 17 i 2 de 32 estigui directament per sobre de 7 de 17.
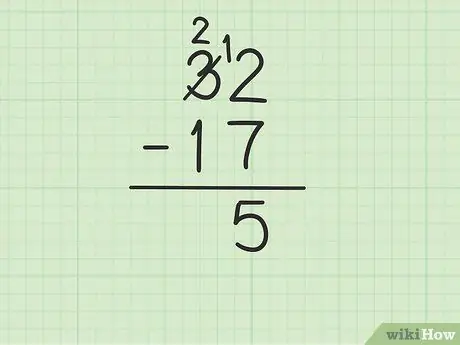
Pas 3. Resteu el número superior de la columna d'unitats del número de la part inferior
Tanmateix, això es pot complicar si el nombre inferior és superior al nombre superior. En aquest cas, el 7 és superior a 2. A continuació, us expliquem què heu de fer:
- Heu de demanar prestat del número 3 de 32 (també conegut com a agrupació), per convertir 2 en 12.
- Creueu el número 3 de 32 i substituïu-lo pel número 2, mentre que el número 2 passa a ser 12.
- Ara podeu restar 12 - 7, que equivalen a 5. Escriviu 5 sota els dos números que resteu perquè estiguin a la columna d'unitats de la nova fila.
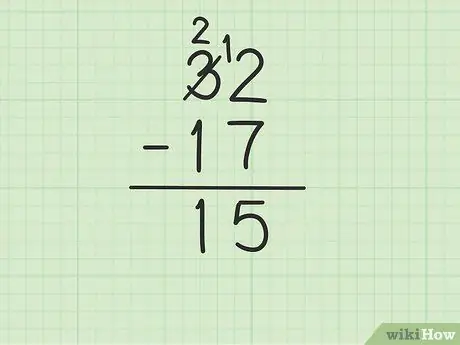
Pas 4. Resteu el número superior de la columna de desenes del número inferior
Recordeu que 3 s’ha convertit en 2. Ara resteu 1 de 17 de 2 per obtenir (2-1) 1. Escriviu 1 a sota, a la columna de desenes, a l’esquerra de 5 a la columna d’unitats. Escrius 15. És a dir, 32 - 17 = 15.
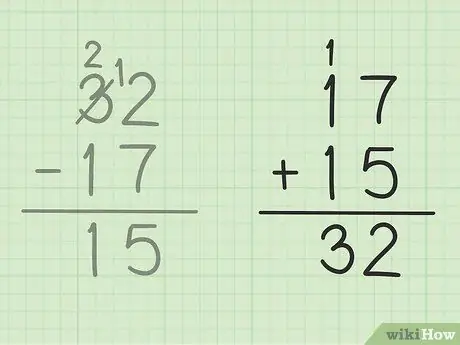
Pas 5. Comproveu el vostre treball
Si voleu assegurar-vos que heu restat dos números correctament, tot el que heu de fer és sumar la resposta amb el nombre més petit per obtenir un nombre gran. En aquest problema, heu d'afegir la resposta 15 al menor nombre de restes, 17. 15 + 17 = 32, de manera que la resposta sigui correcta. Caixa forta!
Mètode 2 de 6: restar nombres sencers petits
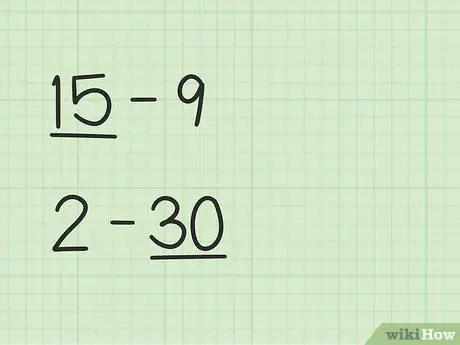
Pas 1. Cerqueu el nombre més gran
Problemes com el 15 -9 tindran una forma diferent de 2-30.
- A les preguntes 15 a 9, el primer número, 15, és més gran que el segon número, 9.
- A les preguntes 2 a 30, el segon número, 30, és més gran que el primer número, 2.
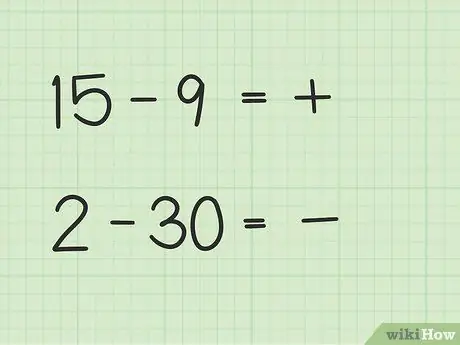
Pas 2. Decidiu si la vostra resposta serà positiva o negativa
Si el primer número és més gran, la resposta és positiva. Si el segon número és més gran, la resposta és negativa.
- A la primera pregunta, del 15 al 9, la vostra resposta és positiva perquè el primer número és superior al segon número.
- A la segona pregunta, de 2 a 30, la vostra resposta és negativa perquè el segon número és superior al primer.
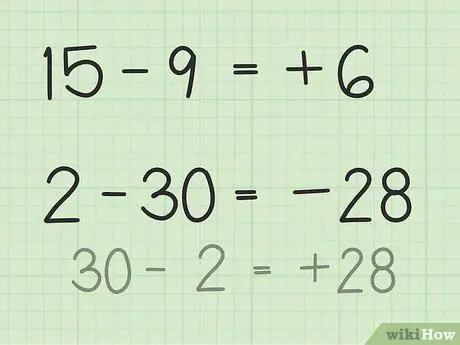
Pas 3. Trobeu la diferència entre dos nombres
Per restar dos nombres, cal imaginar la diferència entre els dos nombres i calcular els nombres entre ells.
- Per a les preguntes 15 a 9, imagineu-vos una pila de 15 fitxes de pòquer. Llenceu 9 fitxes i només 6. Per tant, 15 - 9 = 6. També podeu imaginar una línia numèrica. Penseu en els números de l’1 al 15 i, a continuació, descarteu o torneu 9 unitats per obtenir-ne 6.
- Per a les preguntes 2 a 30, la forma més senzilla de solucionar-ho és invertir el nombre i fer que el resultat sigui negatiu després de restar. Per tant, 30 - 2 = 28, de manera que 28 i 30 tenen una diferència de 2. Ara, feu el resultat negatiu perquè ja heu determinat que la resposta és negativa perquè el segon número és més gran que el primer número. Per tant, 2-30 = -28.
Mètode 3 de 6: restar decimals
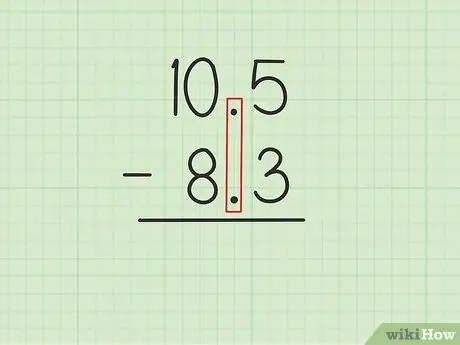
Pas 1. Escriviu el nombre més gran sobre el nombre més petit amb els punts decimals alineats
Suposem que voleu resoldre els problemes següents: 10, 5 - 8, 3. Escriviu 10, 5 sobre 8, 3 de manera que els punts decimals dels dos nombres siguin paral·lels., 5 de 10, 5 ha d'estar directament a sobre, 3 de 8, 3 i 0 de 10, 5 ha de ser superior a 8 de 8, 3.
Si teniu un problema perquè els dos números no tenen el mateix número després del punt decimal, escriviu 0 al blanc fins que la suma dels números sigui la mateixa. Per exemple, el problema és 5, 32 - 4, 2, el podeu escriure com a 5, 32 - 4, 2 0. Això no canviarà el valor del segon número, però facilitarà la resta dels dos números.

Pas 2. Resteu el número superior de la columna de desenes del número següent
En aquest cas, heu de restar 3 de 5. 5 - 3 = 2, de manera que heu d’escriure 2 per 3 de 8, 3.
Assegureu-vos de posar un punt decimal a la resposta, de manera que quedi escrit, 2

Pas 3. Resteu el número que hi ha a sobre de la columna d'unitats del número que hi ha a sota
Heu de restar 8 de 0. Presteu 1 de la part de desenes per canviar de 0 a 10 i resteu de 10 a 8 per obtenir 2. També podeu comptar de 10 a 8 sense demanar prestat perquè no hi ha números a la segona columna de desenes. Escriviu la resposta sota 8, a l’esquerra del punt decimal.

Pas 4. Escriviu el resultat final
El resultat final és 2, 2.

Pas 5. Comproveu el vostre treball
Si voleu assegurar-vos que la resta decimal sigui correcta, tot el que heu de fer és sumar la resposta amb el nombre més petit per fer el nombre més gran. 2, 2 + 8, 3 = 10, 5, de manera que heu acabat.
Mètode 4 de 6: restar fraccions

Pas 1. Alineeu el denominador i el numerador de la fracció
Suposem que voleu resoldre problemes del 13/10 al 3/5. Escriviu el problema de manera que els dos numeradors, 13 i 3 i els dos denominadors, 10 i 5 estiguin oposats. Aquests dos nombres estan separats per un signe de resta. Això us ajudarà a visualitzar el problema i a solucionar-lo amb més facilitat.

Pas 2. Trobeu el mínim comú denominador
El denominador menys comú és el nombre més petit que es pot dividir per dos nombres. En aquest exemple, heu de trobar el denominador comú més petit que sigui divisible per 10 i 5. Trobareu que 10 és el denominador comú més petit per als dos números perquè 10 és divisible per 10 i 5.
Tingueu en compte que el mínim comú denominador de dos nombres no sempre és un d’ells. Per exemple, el denominador comú més petit de 3 i 2 és 6 perquè 6 és el nombre més petit que es pot dividir per dos nombres
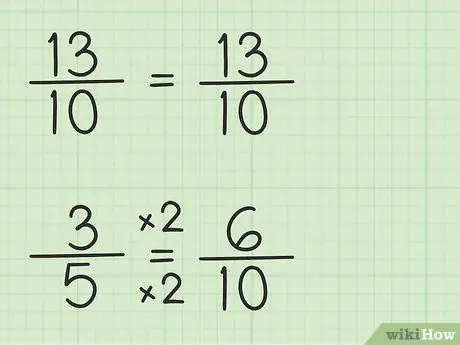
Pas 3. Escriviu les fraccions amb el mateix denominador
La fracció 13/10 es pot escriure de la mateixa manera perquè el denominador és 10, el denominador comú més petit, que és 10, vegades 1. Tanmateix, s’ha de reescriure la fracció 3/5 perquè el denominador és 5, el denominador comú més petit, que és 10, vegades 2. Per tant, la fracció 3/5 s’ha de multiplicar per 2/2 per fer el denominador 10, de manera que 3/5 x 2/2 = 6/10. Heu trobat la fracció equivalent. 3/5 equival a 6/10, tot i que 6/10 permet restar el primer número, 13/10.
Escriviu una nova pregunta com aquesta: 13/10 - 6/10
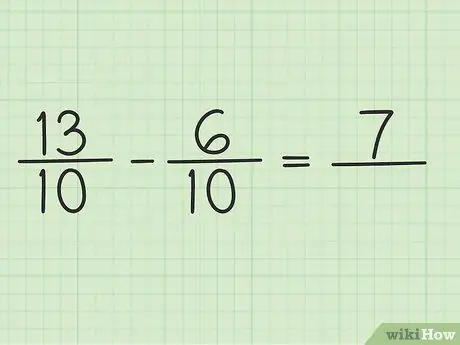
Pas 4. Resteu el numerador a dos números
Només cal restar 13 - 6 perquè el resultat sigui 7. No es pot canviar el denominador de la fracció.
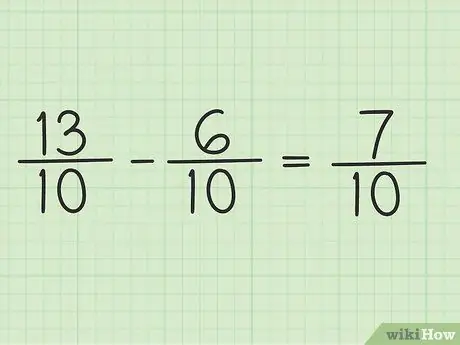
Pas 5. Escriviu el nou numerador sobre el mateix denominador per obtenir el resultat final
El nou numerador és 7. Les dues fraccions tenen un denominador de 10. El resultat final és 7/10.
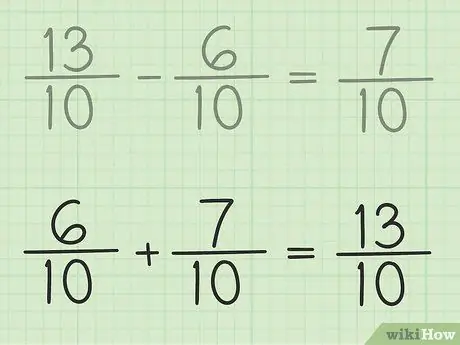
Pas 6. Comproveu el vostre treball
Si voleu assegurar-vos que resteu la fracció correctament, només cal que sumeu la resposta i la fracció més petita perquè el resultat sigui una fracció més gran. 7/10 + 6/10 = 13/10. Ha acabat.
Mètode 5 de 6: restar fraccions de nombres sencers

Pas 1. Escriviu el problema
Per exemple, suposem que voleu resoldre el següent problema: 5 -. Anoti-ho.
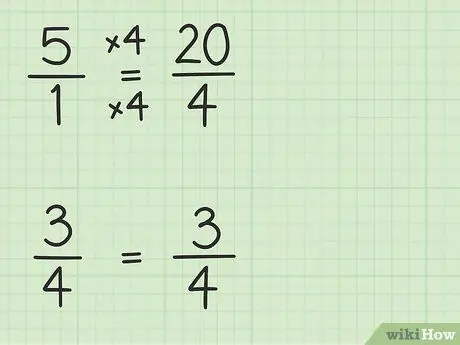
Pas 2. Converteix nombres enters en fraccions que tinguin el mateix denominador que altres fraccions
Converteix el 5 en una fracció amb un denominador de 4 per poder restar dos nombres. Per tant, cal pensar en 5 com a fracció de 5/1. Llavors, podeu multiplicar el numerador i el denominador de la nova fracció per 4 per fer els denominadors dels dos números iguals. Per tant, 5/1 x 4/4 = 20/4. Aquesta fracció és igual a 5, però permet restar dos nombres.
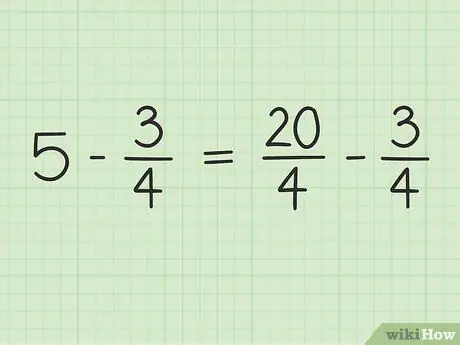
Pas 3. Torneu a escriure el problema
El nou problema es pot escriure així: 20/4 - 3/4.
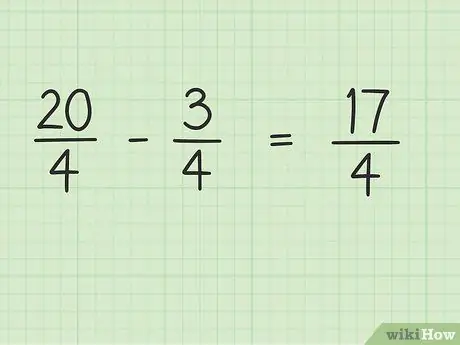
Pas 4. Resteu el numerador de la fracció, mentre que el denominador continua sent el mateix
Ara, només cal restar 20 per 3 per obtenir el resultat final. 20 - 3 = 17, de manera que 17 és el nou numerador. Podeu deixar el denominador igual.
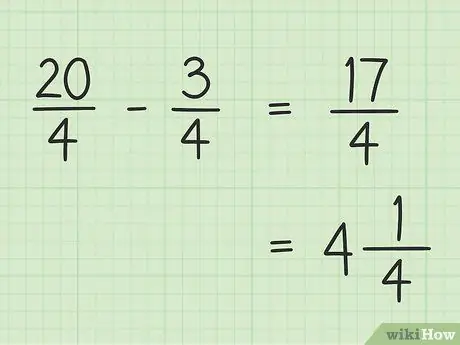
Pas 5. Escriviu el resultat final
El vostre resultat final és el 17/4. Si voleu escriure-ho com un nombre mixt, divideix 17 per 4 de manera que el resultat sigui 4 i la resta sigui 1, de manera que el 17/4 final sigui igual a 4.
Mètode 6 de 6: restar variables
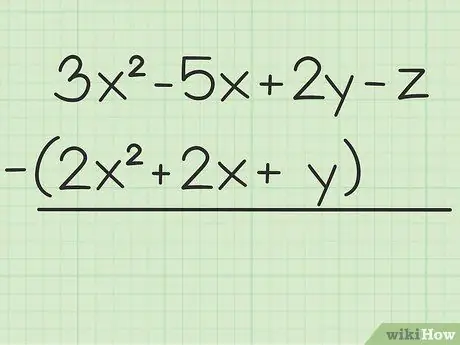
Pas 1. Escriviu el problema que voleu resoldre
Per exemple, la següent pregunta: 3x2 - 5x + 2y - z - (2x2 + 2x + y). Escriviu el primer conjunt de variables sobre el segon.
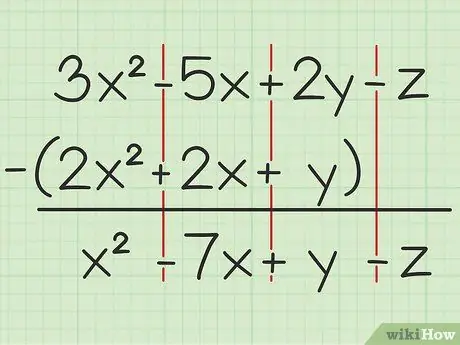
Pas 2. Resteu les mateixes variables
Si us trobeu amb una variable, només podeu afegir o restar la mateixa variable i que s’escriu amb el mateix grau de quadrat. Això vol dir que podeu restar 4x2 des de 7x2, però no es pot restar 4x de 4y. Per tant, podeu desglossar el problema així:
- 3x2 - 2x2 = x2
- -5x - 2x = -7x
- 2y - y = y
- -z - 0 = -z
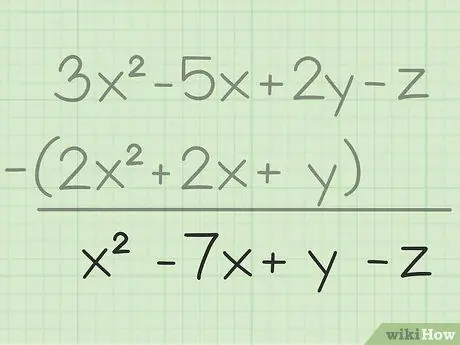
Pas 3. Escriviu el resultat final
Heu restat les mateixes variables, tot el que heu de fer és escriure el resultat final que contindrà totes les variables que heu restat. Aquí teniu el resultat final:






