- Autora Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:12.
- Última modificació 2025-01-23 12:10.
El procés de determinació de la polzada quadrada (escrit com a2) en totes les àrees de les figures bidimensionals solen ser força simples. Per al cas més senzill, quan la figura és un quadrat o quadrilàter, es pot obtenir l'àrea en polzades quadrades mitjançant la fórmula longitud × amplada.
Les àrees d'altres formes planes (cercles, triangles, etc.) es poden calcular mitjançant diverses fórmules matemàtiques. També podeu fer una conversió senzilla de peus quadrats o centímetres quadrats de polzades quadrats, si cal.
Pas
Mètode 1 de 3: determinar polzades quadrades en un quadrat o quadrat
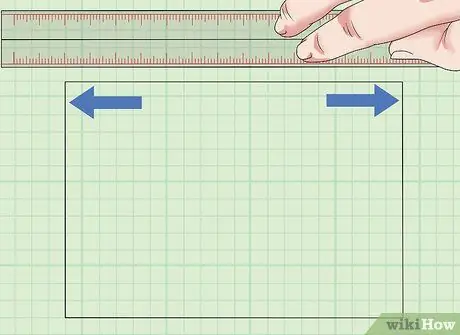
Pas 1. Determineu la longitud de l'àrea a mesurar
Els quadrats i rectangles tenen 4 costats rectes. Un quadrat té quatre costats de la mateixa longitud, mentre que en un rectangle, només els costats oposats tenen la mateixa longitud. Mesureu un costat del quadrat o rectangle per esbrinar el valor de la longitud.
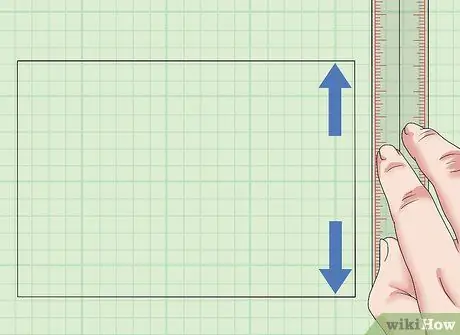
Pas 2. Determineu l'amplada de l'àrea a mesurar
A continuació, mesureu un dels costats al costat del costat mesurat prèviament. Aquest costat hauria de reunir-se amb el primer costat amb un angle de 90 graus. Aquesta és l'amplada del vostre quadrat o rectangle.
Com que els quatre costats del quadrat tenen la mateixa longitud, la "longitud" resultant serà igual a la mesura de "amplada". Per tant, normalment per a un quadrat només cal mesurar un costat
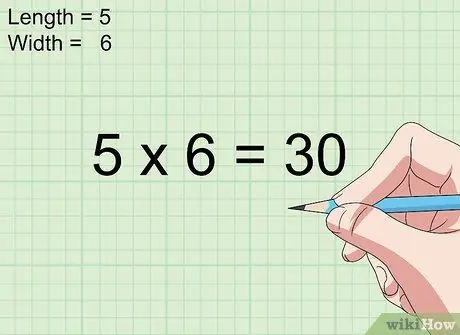
Pas 3. Multipliqueu la longitud i l'amplada
Simplement multipliqueu les mesures de longitud i amplada per determinar l'àrea d'un quadrat o rectangle en polzades al quadrat.
- Per exemple, digueu que el problema demana l’àrea d’un rectangle de 4 polzades de llarg i 3 polzades d’amplada. En aquest cas, l'àrea del rectangle és 4 x 3 = 12 centímetres quadrats.
- De nou, tots els costats del quadrat tenen la mateixa longitud de costat. Per tant, només cal mesurar un costat i multiplicar-lo pel nombre mateix (també conegut com a "quadrat" o per la potència de dos) per obtenir l'àrea en polzades al quadrat.
Mètode 2 de 3: Determinació de polzades quadrades en altres formes planes
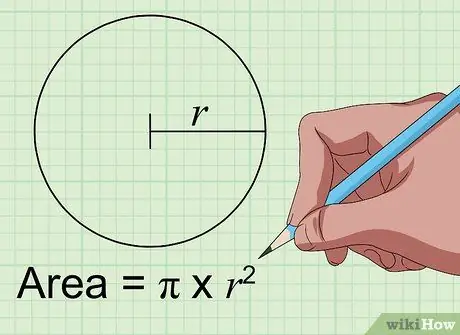
Pas 1. Cerqueu l'àrea d'un cercle mitjançant la fórmula Àrea = pi × r2.
Per trobar l'àrea d'un cercle en polzades quadrades, només heu de conèixer la distància des del centre del cercle fins als seus costats en polzades. Aquesta distància s’anomena “radi” del cercle. Si ho heu obtingut, simplement introduïu el número a la variable "r" de la fórmula anterior. Multiplicar pel nombre mateix, i després multiplicar per la constant pi (3, 1415926 …) per obtenir l'àrea del cercle en polzades al quadrat.
Per tant, un cercle amb un radi de 4 polzades té una àrea de 50,27 polzades al quadrat, que és el producte de 3,14 x 16
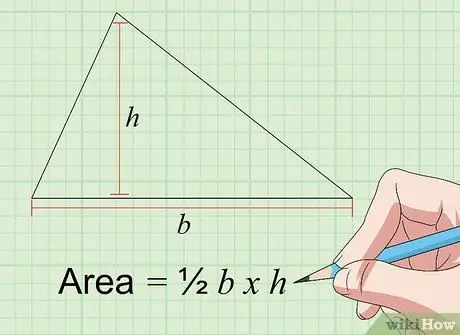
Pas 2. Cerqueu l'àrea del triangle mitjançant la fórmula Àrea = 1/2 a × t
L'àrea d'un triangle en polzades quadrades es pot trobar multiplicant la base ("a") i l'alçada ("t"), ambdues en polzades. La base d'un triangle és la longitud d'un dels seus costats, mentre que l '"alçada" d'un triangle és la distància des del costat de la "base" fins a la cantonada del triangle oposat en un angle de 90 graus. L’àrea d’un triangle es pot calcular si coneixeu les longituds dels costats de la base i les altures dels tres costats i els angles oposats.
Per tant, si trieu un costat de 4 polzades de llarg com a base i l’alçada d’aquest costat de la base és de 3 polzades, l’àrea del triangle és de 2 x 3 = 6 polzades al quadrat
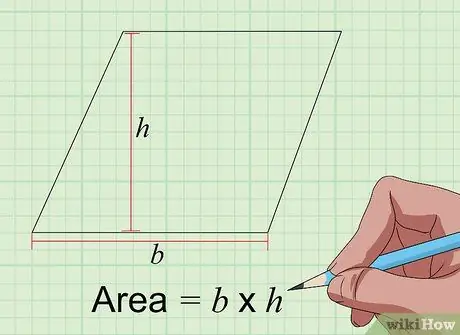
Pas 3. Cerqueu l'àrea del paral·lelogram amb la fórmula Àrea = a × t
Un paral·lelogram és similar a un rectangle, però els costats no es troben en un angle de 90 graus. Tanmateix, la manera de trobar l'àrea d'un paral·lelogram en polzades quadrades és la mateixa que la d'un rectangle, multiplicant la base per l'alçada en polzades. La base és la longitud d’un dels seus costats, mentre que l’alçada és la distància des del costat de la base fins al costat oposat amb un angle de 90 graus.
Per tant, si la longitud del costat seleccionat és de 5 polzades i després de mesurar l’alçada fa 4 polzades de llarg, l’àrea és de 5 x 4 = 20 polzades al quadrat
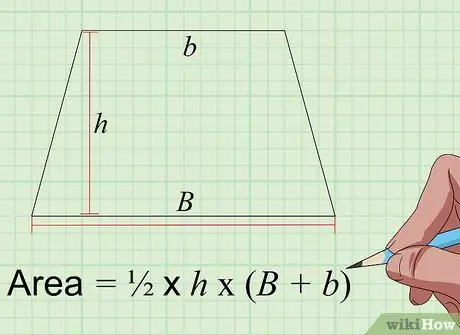
Pas 4. Cerqueu l'àrea del trapezi amb la fórmula Àrea = 1/2 × t × (A + a)
Un trapezi és una forma plana de 4 cares amb un parell de costats paral·lels i els altres costats no paral·lels. Per calcular l'àrea d'un trapezi en polzades quadrades, heu de conèixer 3 mesures en polzades, respectivament, la longitud del costat paral·lel llarg ("A"), el costat paral·lel més curt ("a") i l'alçada del trapezi ("t")., és a dir, la distància entre dos costats paral·lels mesurats en angles de 90 graus. Afegiu les longituds dels dos costats paral·lels, multipliqueu per l'alçada i, a continuació, dividiu-la per dos per obtenir l'àrea del trapezoide en polzades al quadrat.
Per exemple, si els costats paral·lels d’un trapezoide fan 6 polzades de llarg, els costats paral·lels curts són de 4 polzades i l’alçada de 5 polzades, l’àrea és de 5 x (6 + 4) = 25 polzades quadrades
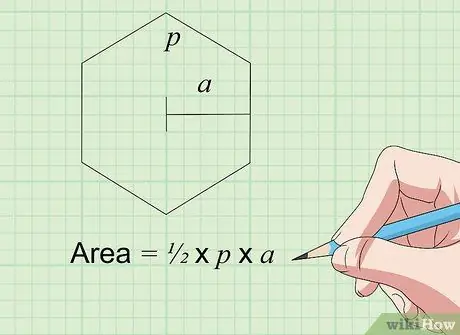
Pas 5. Cerqueu l'àrea de l'hexàgon (hexàgon) amb la fórmula Àrea = × K × s
Aquesta fórmula funciona per a tots els hexàgons regulars, que són formes planes que tenen 6 costats iguals i 6 angles iguals. K és el perímetre o longitud del costat multiplicat per 6 (6 x s) per a un hexàgon regular. La variable a representa l'apotema, que és la longitud des del centre de l'hexàgon fins a un dels seus costats (el punt mig del costat entre els dos angles). Multiplicar i dividir el resultat per trobar l'àrea de l'hexàgon.
Per tant, si un hexàgon amb els sis costats fa 4 polzades de llarg (el que significa K = 6 x 4 = 24) i l’apotema fa 3,5 polzades de llarg, l’àrea és de 24 x 3,5 = 42 polzades quadrades
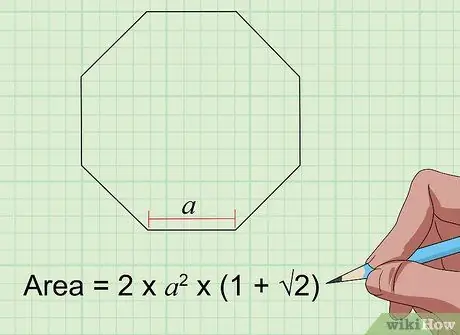
Pas 6. Cerqueu l'àrea de l'octàgon amb la fórmula Àrea = 2s² × (1 + 2)
Per a un octàgon regular (que té 8 costats iguals i 8 angles), només cal conèixer la longitud d'un costat ("s" a la fórmula) per trobar l'àrea. Connecteu els valors a la fórmula i calculeu-los per obtenir l’àrea de l’octàgon.
Si el vostre octàgon normal té una longitud lateral de 4 polzades, la seva àrea és de 2 (16) x (1 + 1, 4) = 32 x 2,4 = 76,8 polzades quadrades
Mètode 3 de 3: convertir altres unitats a polzades quadrades

Pas 1. Canvieu la mida a polzades abans de calcular
Per obtenir una resposta final en polzades quadrades, es recomana convertir tots els valors que es calculin en polzades (com ara la longitud, l'alçada o l'apotema). Per tant, si els costats del quadrat són d’1 peu cadascun, converteix-los a 12 polzades abans de calcular l’àrea. Normalment s’utilitzen els següents factors de conversió per convertir a polzades:
- 1 peu = 12 polzades
- 1 jardí = 36 polzades
- 1 centímetre = 0,3937 polzades
- 1 metre = 39.3701 polzades
- 1 mil·límetre = 0,0394 polzada
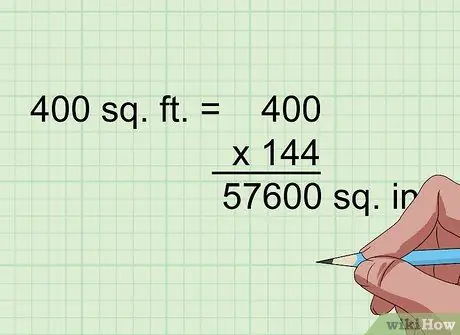
Pas 2. Multiplicar per 144 per convertir els peus quadrats a polzades quadrades
1 peu quadrat és 1 peu quadrat (1 peu per 1 peu); el que significa que 12 polzades quadrades també equivalen a 12 polzades per 12 polzades, cosa que fa 144 polzades al quadrat. Per tant, si una forma plana té una superfície en peus quadrats, simplement multipliqueu-la per 144 per convertir-la en polzades quadrades.
Per exemple, 400 peus quadrats = 400 x 144 = 57.600 polzades al quadrat
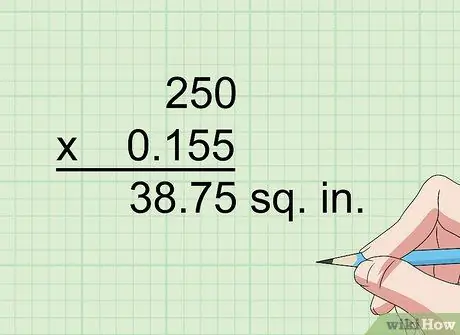
Pas 3. Multipliqueu per 0,155 per convertir centímetres quadrats a polzades quadrades
Un centímetre equival a 0,394 polzades i 0,394 quadrats (0,394 x 0,394) equival a 0,155. Així, per exemple, si heu de convertir 250 centímetres quadrats a polzades quadrades, multipliqueu 250 per 0,155 per obtenir 38,75 polzades al quadrat.






