- Autora Jason Gerald [email protected].
- Public 2023-12-16 11:00.
- Última modificació 2025-01-23 12:10.
És fàcil trobar l’arrel quadrada d’un nombre si la resposta és un nombre enter. Si la resposta no és un nombre enter, hi ha una sèrie de processos que podeu seguir per obtenir l'arrel quadrada, fins i tot si no utilitzeu una calculadora. Per a això, heu d’entendre els fonaments de la multiplicació, la suma i la divisió.
Pas
Mètode 1 de 3: trobar l’arrel quadrada d’un enter
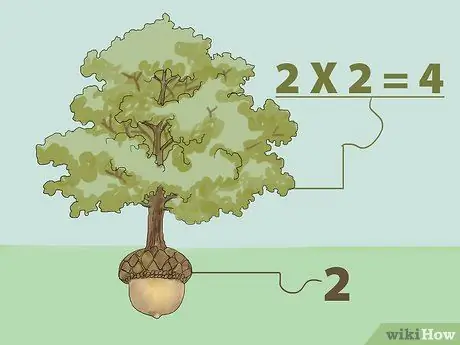
Pas 1. Trobeu l’arrel quadrada perfecta multiplicant-la
L'arrel quadrada d'un nombre és un número que, multiplicat per si mateix, retorna el nombre original. En altres paraules: "Quin nombre podem multiplicar per si mateix per obtenir el nombre que volem?"
- Per exemple, l'arrel quadrada d'1 és 1 perquè 1 multiplicat per 1 és 1 (1X1 = 1). Per tant, l’arrel quadrada de 4 és 2 perquè 2 multiplicat per 2 és 4 (2X2 = 4). Penseu en el concepte d’arrel quadrada com un arbre. Un arbre creix a partir de llavors. Per tant, un arbre és més gran que una llavor, que creix a partir d’una llavor que és la seva arrel. De l'exemple anterior, 4 és l'arbre i 2 és la llavor.
- Per tant, l’arrel quadrada de 9 és 3 (3X3 = 9), de 16 és 4 (4X4 = 16), de 25 és 5 (5X5 = 25), de 36 és 6 (6X6 = 36), de 49 és 7 (7X7 = 49), de 64 és 8 (8X8 = 64), de 81 és 9 (9X9 = 81) i de 100 és 10 (10X10 = 100).
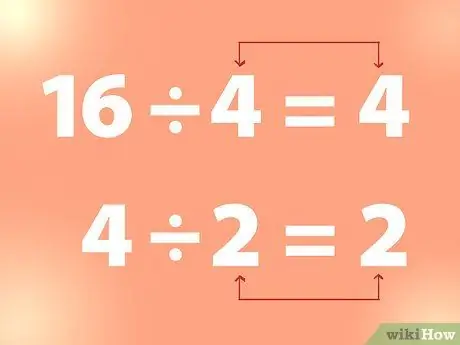
Pas 2. Utilitzeu la divisió contínua per trobar l'arrel quadrada
Per trobar l’arrel quadrada d’un enter, podeu dividir l’enter per un nombre fins obtenir un nombre que sigui igual al divisor.
- Exemple: 16 dividit per 4 és 4. I 4 dividit per 2 és 2, etc. Així, a partir de l’exemple anterior, 4 és l’arrel quadrada de 16 i 2 és l’arrel quadrada de 4.
- Les arrels quadrades perfectes no tenen fraccions ni decimals perquè són nombres enters.
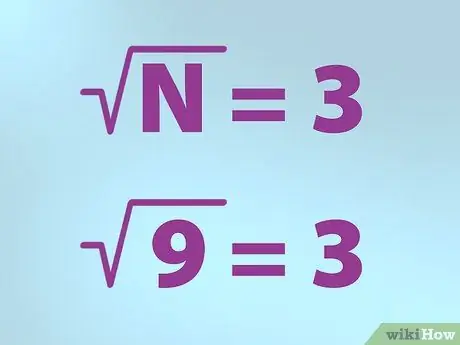
Pas 3. Utilitzeu el símbol correcte per a l'arrel quadrada
Els matemàtics utilitzen un símbol especial per representar l’arrel quadrada. La forma és com una marca de verificació amb més una línia a la part superior dreta.
- N és igual al nombre per al qual voleu trobar l'arrel quadrada. N es col·loca sota la marca de verificació.
- Per tant, si voleu trobar l’arrel quadrada de 9, escriviu una fórmula posant "N" (9) dins d'una marca de verificació (símbol "arrel"), escriviu un signe igual i seguit de 3. Significa "arrel quadrada de 9 és igual a 3 ".
Mètode 2 de 3: trobar l’arrel quadrada d’un altre número
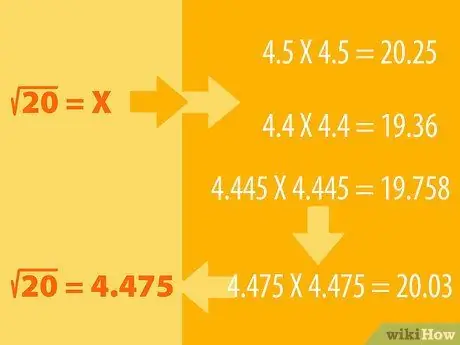
Pas 1. Endevina i fes el procés d’eliminació
És difícil trobar l’arrel quadrada d’un nombre no enter. Tot i això, això no vol dir que sigui impossible.
- Per exemple, suposem que voleu trobar l’arrel quadrada de 20. Sabem que 16 és un quadrat perfecte l’arrel quadrada de la qual és 4 (4X4 = 16). Aleshores les 25 arrels quadrades són 5 (5X5 = 25), de manera que l’arrel quadrada de 20 ha d’estar entre les dues.
- Podeu endevinar que l’arrel quadrada de 20 és 4,5. Ara és 4,5 per veure el resultat. És a dir, multiplicem 4, 5 per si mateix: 4, 5X4, 5. Mireu si la resposta és més o menys de 20. Si la vostra suposició és massa llunyana, proveu un altre número (per exemple, 4, 6 o 4, 4) i ajusteu-ho endevineu-ho en conseqüència, fins que obtingueu el número 20.
- Per exemple, 4, 5X4, 5 = 20, 25, de manera que lògicament hem de trobar un nombre menor, potser 4, 4. 4, 4X4, 4 = 19, 36. Per tant, l’arrel quadrada de 20 ha d’estar entre 4, 5 i 4, 4. Proveu amb 4, 445X4, 445. El resultat és 19, 758. El resultat és cada vegada més a prop. Continueu provant amb altres números fins que obtingueu 4, 475X4, 475 = 20, 03. Arrodonit, aquest nombre és igual a 20.

Pas 2. Utilitzeu el procés de mitjana
Aquest procés també comença trobant els dos quadrats perfectes més propers que estan flanquejats pel nombre.
- A continuació, dividiu aquest nombre per una de les arrels quadrades perfectes. Agafeu la resposta i, a continuació, busqueu la mitjana entre aquest nombre i el nombre del qual voleu trobar l'arrel (podeu trobar la mitjana sumant els dos junts i dividint-los per dos). A continuació, divideix el nombre inicial per la mitjana obtinguda. L'últim pas, cerqueu la mitjana dels resultats amb la mitjana calculada la primera vegada.
- Sona complicat? Seria més fàcil donar-ne un exemple. Per exemple, 10 es troba entre els dos quadrats perfectes 9 (3X3 = 9) i 16 (4X4 = 16). Les arrels quadrades de tots dos nombres són 3 i 4. Per tant, divideix 10 pel primer nombre, 3. El resultat és 3, 33. Ara troba la mitjana de 3 i 3, 33 sumant-les i dividint per 2. El resultat és 3, 1667 Ara divideix 10 per 3,1667. El resultat és 3,1579. A continuació, trobeu la mitjana de 3,1579 i 3,1667 sumant-los i dividint per 2. El resultat és 3,1623.
- Comproveu el resultat multiplicant la resposta (en aquest exemple 3, 1623) per si mateixa. El resultat de 3,1623 multiplicat per 3,1623 resulta ser 10,001.
Mètode 3 de 3: quadració de nombres negatius
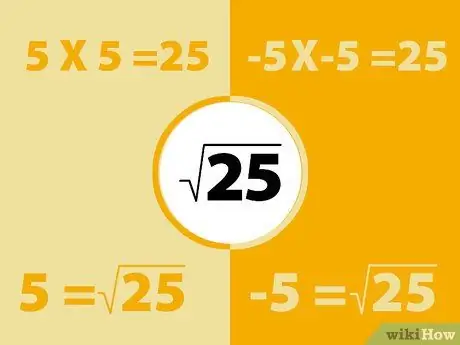
Pas 1. Nombres negatius quadrats amb el mateix mètode
Recordeu que el temps negatiu negatiu és positiu. Per tant, el quadrat d’un nombre negatiu produirà un nombre positiu.
- Per exemple, -5X-5 = 25. Tanmateix, recordeu també que 5x5 = 25. Per tant, l’arrel quadrada de 25 pot ser -5 o 5. Bàsicament cada nombre té dues arrels quadrades.
- De la mateixa manera, 3X3 = 9 i -3X-3 = 9, de manera que les arrels quadrades de 9 són 3 i -3. L'arrel quadrada positiva s'anomena "arrel principal". En aquest moment, només hem de prestar atenció a aquesta resposta.
Pas 2. Utilitzeu una calculadora
Tot i que el millor és poder fer les matemàtiques a mà, hi ha moltes calculadores en línia disponibles per calcular les arrels quadrades.
- Cerqueu el botó d’arrel quadrada en una calculadora normal.
- A la calculadora en línia, introduïu directament el número per al qual voleu trobar el valor de l'arrel quadrada i feu clic al botó. L’ordinador us mostrarà el valor de l’arrel quadrada.
Consells
-
Tingueu sempre presents alguns quadrats perfectes importants:
- 02 = 0, 12 = 1, 32 = 9, 42 = 16, 52 = 25, 62 = 36, 72 = 49, 82 = 64, 92 = 81, 102 = 100,
- Recordeu també aquest quadrat perfecte: 112 = 121, 122 = 144, 132 169, 142 = 196, 152 = 225, 162 = 256, 172 = 289…
- Tingueu en compte també això: 102 = 100, 202 = 400, 302 = 900, 402 = 1600, 502 = 2500, …






