- Autora Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:12.
- Última modificació 2025-01-23 12:09.
Tothom pot aprendre matemàtiques, ja sigui que estigui en una etapa superior de l’escola o que vulgui tornar a perfeccionar els conceptes bàsics. Després de discutir com ser un bon estudiant de matemàtiques, aquest article us ensenyarà les progressions bàsiques de les matemàtiques i us proporcionarà els elements bàsics que haureu d’aprendre en cada pràctica. A continuació, en aquest article es debatran els conceptes bàsics de l'aprenentatge de l'aritmètica, que ajudaran tant als nens de l'escola primària com a tothom que vulgui aprendre els conceptes bàsics d'aquest camp de la ciència.
Pas
Primera part de 6: claus per convertir-se en un bon estudiant de matemàtiques

Pas 1. Apareix a classe
Quan us perdeu la classe, heu d’aprendre conceptes dels companys o del vostre llibre de text. Mai no obtindreu resums de text d’un amic tant com obtingueu del vostre professor.
- Vine a classe a temps. En lloc d’això, arribeu una mica aviat i obriu la llibreta al lloc adequat, obriu el llibre de text i traieu la calculadora perquè pugueu començar quan el vostre professor estigui a punt per ensenyar.
- Només absent si està malalt. Si realment trobeu a faltar a la classe, demaneu als companys que esbrinin de què parlava el professor i quines tasques li van donar.

Pas 2. Treballa amb el teu professor
Si el vostre professor treballa en un problema davant de la classe, treballeu amb el professor treballant el problema a la vostra llibreta.
- Assegureu-vos que les vostres notes siguin clares i fàcils de llegir. No només escrigui preguntes. Escriviu també qualsevol cosa que digui el professor que pugui millorar la vostra comprensió dels conceptes que s’expliquen.
- Completa les preguntes de mostra del teu professor. Mentre el professor camina per la classe mentre treballa, respon a les preguntes que se li fan.
- Participa quan el professor resolgui un problema. No espereu que el professor us truqui. Oferiu-vos de respondre quan en conegueu la resposta i aixequeu la mà per fer una pregunta si no esteu segur del material que s’ensenya.

Pas 3. Feu els deures el mateix dia que els doneu els deures
Si feu els deures el mateix dia, el concepte encara us és fresc. De vegades, no és possible acabar els deures el mateix dia. Assegureu-vos que els deures s’acabin abans d’anar a classe.

Pas 4. Treballeu fora de classe si necessiteu ajuda
Visiteu el vostre professor durant els descansos o en horari d’oficina.
- Si teniu un centre de matemàtiques a la vostra escola, informeu-vos de l’horari d’obertura i demaneu ajuda.
- Uniu-vos a un grup d’estudi. Un bon grup d’estudi consisteix generalment en 4 o 5 persones amb diferents nivells de capacitat. Si sou estudiants de "C" a Matemàtiques, uniu-vos a un grup de 2 o 3 estudiants amb qualificacions "A" o "B" perquè pugueu millorar les vostres habilitats. Eviteu unir-vos a un grup d'estudiants les qualificacions dels quals siguin inferiors a la vostra.
Part 2 de 6: Aprendre matemàtiques a l’escola

Pas 1. Comenceu amb l'aritmètica
A la majoria de les escoles, els estudiants aprenen aritmètica a l'escola primària. L’aritmètica cobreix els conceptes bàsics de suma, resta, multiplicació i divisió.
- Feu preguntes pràctiques. Fer una vegada i una altra problemes aritmètics és la millor manera de memoritzar els conceptes bàsics correctament. Cerqueu programari que us pugui oferir una gran varietat de problemes matemàtics. A més, busqueu problemes amb els terminis per millorar la vostra velocitat.
- També podeu trobar problemes d’aritmètica en línia i podeu descarregar aplicacions d’aritmètica al dispositiu mòbil.

Pas 2. Continueu amb la preàlgebra
Aquest exercici us proporcionarà els elements bàsics que necessitareu per resoldre problemes d’àlgebra més endavant.
- Coneix les fraccions i decimals. Aprendràs a sumar, restar, multiplicar i dividir fraccions i decimals. Respecte a les fraccions, aprendreu a restar fraccions i traduir nombres combinats. Pel que fa als decimals, entendreu els valors del lloc i podreu utilitzar els decimals en els problemes de la història.
- Obteniu informació sobre les proporcions, les proporcions i els percentatges. Aquests conceptes us ajudaran a fer comparacions.
- Presenteu-vos a la geometria bàsica. Aprendràs formes i conceptes en 3D. També aprendràs conceptes com àrea, perímetre, volum i superfície, així com informació sobre línies i angles paral·lels i perpendiculars.
- Comprendre algunes estadístiques bàsiques. A la preàlgebra, la vostra introducció a les estadístiques inclou generalment visuals com ara gràfics, gràfics de dispersió, gràfics de gràfics de segells i histogrames.
- Aprendre els conceptes bàsics de l’àlgebra. Això inclou conceptes com resoldre equacions simples que contenen variables, conèixer propietats com la propietat distributiva, dibuixar equacions simples i resoldre desigualtats.
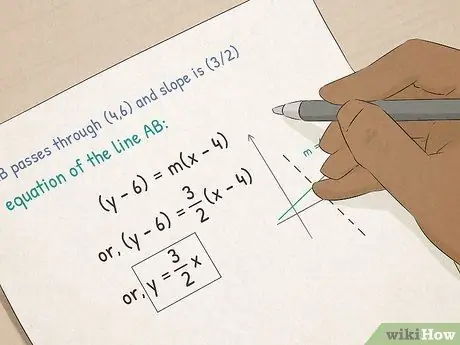
Pas 3. Avanç a l'àlgebra I
Al vostre primer any d’àlgebra, coneixereu els símbols bàsics inclosos a l’àlgebra. També aprendràs a:
- Resoldre equacions i desigualtats que contenen variables. Aprendràs a resoldre aquests problemes en paper i a resoldre'ls amb imatges.
- Resoldre problemes de la història. Us sorprendrà el nombre de problemes quotidians que afrontareu en el futur que requereixen la capacitat de resoldre problemes algebraics de la història. Per exemple, utilitzaríeu l'àlgebra per esbrinar el tipus d'interès que guanyeu al vostre compte bancari o inversió. També podeu utilitzar l’àlgebra per esbrinar quant de temps heu de viatjar en funció de la velocitat del vostre cotxe.
- Treballar amb exponents. Quan comenceu a resoldre equacions polinòmiques (expressions que contenen nombres i variables), entendreu com utilitzar exponents. Probablement inclourà exercicis amb notació científica. Un cop dominats els exponents, podeu aprendre a sumar, restar, multiplicar i dividir expressions polinòmiques.
- Resoldre problemes d’arrel quadrada i quadrada. En dominar aquest tema, podreu memoritzar els quadrats de molts números. També podreu treballar amb equacions que tenen arrels quadrades.
- Comprendre funcions i gràfics. En àlgebra, aprendràs sobre equacions gràfiques. Aprendràs a calcular el pendent d’una línia, a posar una equació en forma de punt-inclinació i a calcular la llesca xyy d’una línia mitjançant la forma d’intercepció de pendent.
- Esbrineu el sistema d’equacions. De vegades, se us proporcionen dues equacions diferents amb les variables x i y, i heu de resoldre per x o y per a ambdues equacions. Afortunadament, aprendreu molts trucs per resoldre aquestes equacions, incloses la representació gràfica, la substitució i la suma.

Pas 4. Estudi de la geometria
En geometria, coneixereu les propietats de les línies, segments, angles i formes.
- Memoritzareu diversos teoremes i corol·lars que us ajudaran a entendre les regles de la geometria.
- Aprendràs a calcular l’àrea d’un cercle, a utilitzar el teorema de Pitàgores i a trobar la relació entre els angles i els costats d’un triangle especial.
- Veureu moltes preguntes de geometria en futures proves estandarditzades com el SAT, ACT i GRE.
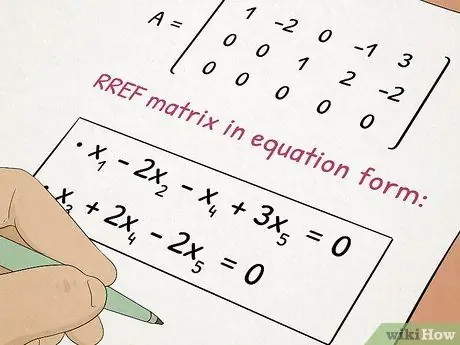
Pas 5. Feu la classe d'Algebra II
Àlgebra II es basa en els conceptes que heu après a l’Àlgebra I alhora que afegiu a temes complexos com ara equacions de segon grau i matrius.
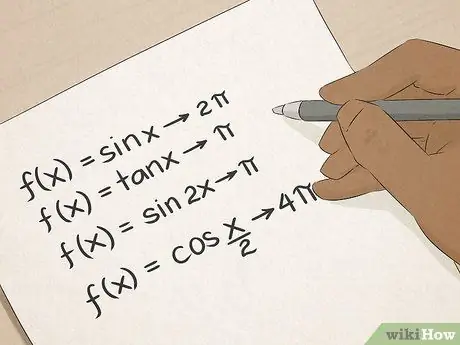
Pas 6. Mestre trigonometria
Sabeu termes trigonomètrics: sinus, cosinus, tangent, etc. La trigonometria us ensenyarà moltes maneres pràctiques de calcular angles i longituds de línia, i aquestes habilitats seran inestimables per a les persones que treballen en construcció, arquitectura, enginyeria o topografia.
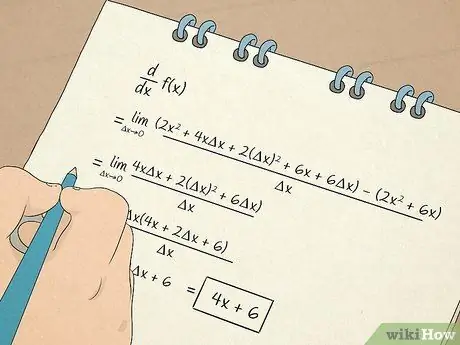
Pas 7. Realitzeu càlculs de càlcul
El càlcul pot semblar intimidatori, però és una meravellosa eina per entendre el comportament dels números o el món que l’envolta.
- El càlcul us ensenyarà funcions i límits. Veureu el comportament numèric de les funcions útils, incloses les funcions e ^ x i logarítmiques.
- També aprendreu a calcular i treballar amb derivats. La primera derivada us proporciona informació basada en el pendent de la recta tangent a una equació. Per exemple, una derivada us indica la velocitat amb què canvia alguna cosa en una situació no lineal. La segona derivada us indicarà si la funció augmenta o disminueix durant un interval determinat per poder determinar la concavitat d’una funció.
- Els integrals us ensenyaran a calcular l'àrea sota una corba, així com el seu volum.
- El càlcul a l’institut generalment acaba en seqüències i seqüències. Tot i que els estudiants no veuran moltes aplicacions per als circuits, els circuits són importants per a aquells que estudien equacions diferencials.
Part 3 de 6: Fonaments matemàtics: addició de màster

Pas 1. Comenceu per fets "+1"
Si afegiu 1 a un número, arribareu al número més alt de la línia numèrica. Per exemple, 2 + 1 = 3.
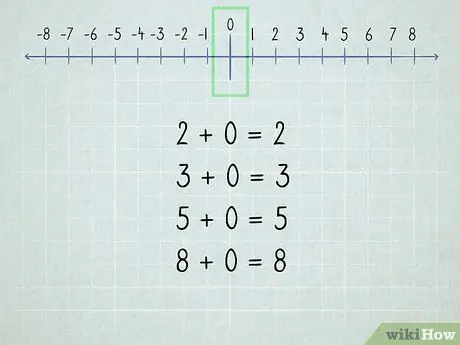
Pas 2. Comprendre el zero
Tots els números afegits a zero són el mateix perquè "zero" significa "cap".

Pas 3. Apreneu números dobles
Els nombres múltiples són un problema que consisteix a afegir dos nombres iguals. Per exemple, 3 + 3 = 6 és un exemple d'una equació que implica múltiples nombres.

Pas 4. Utilitzeu el mapatge per obtenir més informació sobre altres solucions addicionals
A l'exemple següent, apreneu mapant què passa quan afegiu 3 a 5, 2 i 1. Proveu el problema "afegeix per 2" vosaltres mateixos.

Pas 5. Continueu fins que el nombre sigui superior a 10
Apreneu a afegir 3 números junts per obtenir un nombre superior a 10.
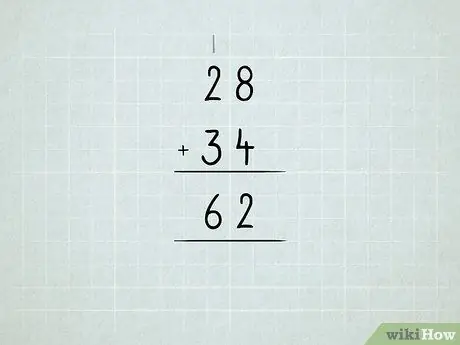
Pas 6. Sumeu els números més grans
Obteniu informació sobre com reagrupar unitats en desenes, desenes en centenars, etc.
- Sumeu primer els números de la columna dreta. 8 + 4 = 12, el que significa que teniu 1 número 10 i 2 número 1. Escriviu el número 2 a la columna d'unitats.
-
Escriviu el número 1 a la columna de desenes.
-
Sumeu la columna de desenes en la seva totalitat.
Part 4 de 6: Fonaments matemàtics: estratègies de reducció

Pas 1. Comenceu amb "1 dígit cap enrere
Si restes 1 d'un número es torna 1 número. Per exemple, 4 - 1 = 3.

Pas 2. Apreneu a restar nombres dobles
Per exemple, afegiu els números 5 + 5 per obtenir 10. Només heu d’escriure l’equació cap enrere per obtenir 10 - 5 = 5.
- Si 5 + 5 = 10, llavors 10 - 5 = 5.
-
Si 2 + 2 = 4, llavors 4 - 2 = 2.

Pas 3. Memoritzeu la família de fets
Com un exemple:
- 3 + 1 = 4
- 1 + 3 = 4
- 4 - 1 = 3
- 4 - 3 = 1

Pas 4. Cerqueu els números que falten
Per exemple, _ + 1 = 6 (la resposta és 5).

Pas 5. Memoritzeu el fet de la resta a 20

Pas 6. Practicar la resta de números de 1 dígit de números de 2 dígits sense demanar prestat
Resteu els números de la columna i reduïu els números de la columna de desenes.
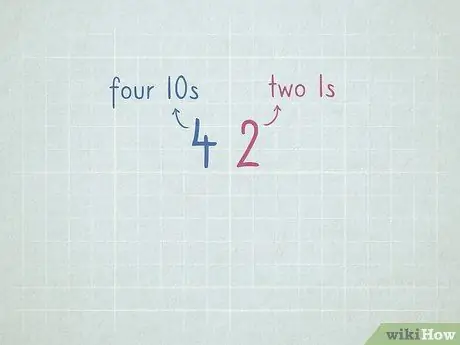
Pas 7. Practicar el valor del lloc per preparar-se per restar en préstecs
- 32 = 3 números 10 i 2 números 1.
- 64 = 6 números 10 i 4 números 1.
- 96 = _ número 10 i _ número 1.
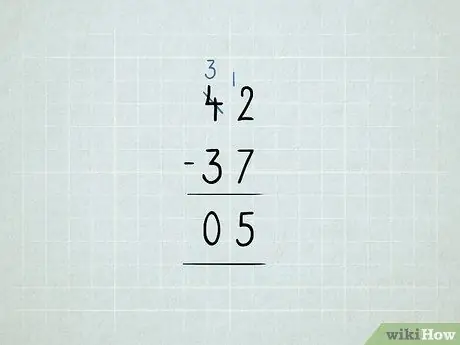
Pas 8. Restar en préstec
- Voleu restar 42 - 37. Comenceu provant de restar 2 - 7 a la columna d'unitats. Resulta que no va funcionar!
-
Préstec el número 10 de la columna de les desenes i col·loqueu-lo a la columna dels. Ara teniu 3 10 en lloc de 4 10. Ara teniu 12 1 en lloc de 2 1.
-
Resteu primer la columna de les vostres unitats: 12 - 7 = 5. Després, comproveu la columna de les desenes. Com que 3 - 3 = 0, no cal que escriviu el número 0. La vostra resposta és 5.
Part 5 de 6: Fonaments matemàtics: multiplicació del màster

Pas 1. Comenceu pel número 1 i el número 0
Tots els números que es multipliquen per 1 són el mateix que el nombre en si. Qualsevol nombre multiplicat per 0 és igual a zero.

Pas 2. Memoritzeu la taula de multiplicar

Pas 3. Pràctica amb problemes de multiplicació d'un sol dígit

Pas 4. Multipliqueu el número de 2 dígits pel número de 1 dígit
- Multipliqueu el número inferior dret pel número superior dret.
-
Multipliqueu el número inferior dret pel número superior esquerre.
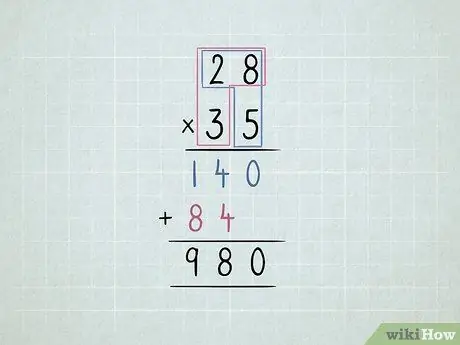
Pas 5. Multiplicar 2 números de 2 dígits
- Multipliqueu el número inferior dret pel número superior dret i després pel número superior esquerre.
-
Moveu la segona fila un dígit cap a l'esquerra.
- Multipliqueu el número inferior esquerre pel número superior dret i després el número superior esquerre.
-
Sumeu totes les columnes.
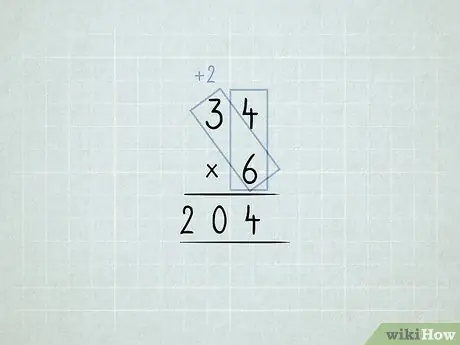
Pas 6. Multiplicar i reagrupar les columnes
- Voleu multiplicar 34 x 6. Comenceu multiplicant la columna d'unitats (4 x 6), però no podeu tenir 24 1 a la columna d'uns.
-
Emmagatzemeu 4 1 s a la columna d'unitats. Moveu 2 10s a la columna de desenes.
-
Multipliqueu 6 x 3, que equival a 18. Afegiu els 2 que heu mogut, que equivalen a 20.
Part 6 de 6: Fonaments matemàtics: revelar problemes de divisió

Pas 1. Penseu en la divisió en lloc de la multiplicació
# * Si 4 x 4 = 16, llavors 16/4 = 4.
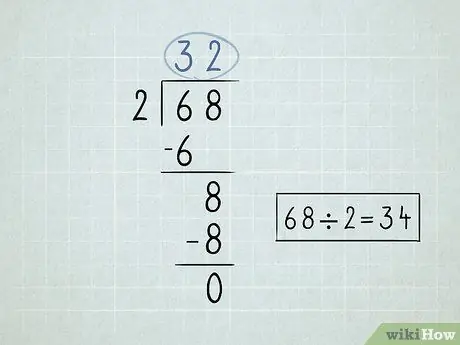
Pas 2. Escriviu el problema de divisió
- Divideix el número a l'esquerra del símbol de divisió, o divisor, pel primer número situat sota el símbol del divisor. Com que 6/2 = 3, escriuríeu el número 3 a sobre del símbol de divisió.
-
Multipliqueu el número que hi ha a sobre del símbol de divisió pel divisor. Baixeu el resultat a la part inferior del primer número sota el símbol de divisió. Com que 3 x 2 = 6, baixareu el número 6 cap avall.
- Resteu els 2 números que heu escrit. 6 - 6 = 0. Podeu deixar 0 en blanc, perquè generalment no comenceu els números amb 0.
-
Baixeu el segon número que hi ha a sota del símbol de divisió.
- Divideix el divisor el nombre que fas caure. En aquest cas, 8/2 = 4. Escriviu el número 4 a sobre del símbol de divisió.
-
Multiplicar el nombre superior dret pel divisor i reduir el nombre. 4 x 2 = 8.
-
Resteu aquests números. La resta final retorna zero, cosa que significa que heu resolt el problema. 68 x 2 = 34.

Pas 3. Calculeu també la resta
Alguns dels divisors no es divideixen completament en altres nombres. Si heu completat l'última resta i no teniu més números per obtenir, l'últim número és la resta.






