- Autora Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-19 22:11.
- Última modificació 2025-01-23 12:09.
Arrodonir els números és una habilitat important a aprendre quan es tenen equacions matemàtiques o problemes de càlcul al món real. Tot i que són menys precisos que els números sense arrodonir, els resultats arrodonits són més fàcils de calcular i imaginar. Podeu arrodonir nombres enters, decimals i fraccions tenint en compte alguns consells clau quan es treballa en equacions o problemes matemàtics. També podeu utilitzar una calculadora o un full de càlcul d'Excel per arrodonir els números i comprovar-ne de nou els resultats.
Pas
Mètode 1 de 6: entendre l'arrodoniment

Pas 1. Redoneu el número per facilitar el càlcul
Si teniu un número amb un nombre decimal prou llarg, per descomptat, serà difícil quan hàgiu de calcular-lo. Aquestes xifres també són difícils de calcular al món real (per exemple, quan es fa pressupost o es compra). Per tant, l’arrodoniment és un mètode per obtenir el nombre aproximat d’un nombre i facilitar el càlcul.
Us podeu imaginar l’arrodoniment com una aproximació matemàtica

Pas 2. Determineu el valor de lloc que voleu arrodonir
Quan arrodoneu un número, podeu arrodonir-lo a qualsevol valor de lloc. Com més petit sigui el valor de lloc al qual estigueu arrodonit, més precís serà el vostre resultat d'arrodoniment.
Per exemple, teniu el número "813, 265". Podeu arrodonir a un valor local de centenars, desenes, uns, dècims o centèsimes
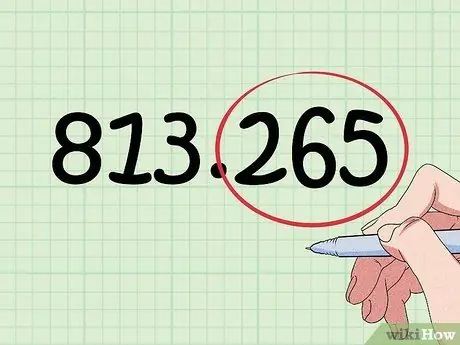
Pas 3. Observeu el dígit a la dreta del valor de lloc que voleu arrodonir
Per exemple, si voleu arrodonir al lloc de les desenes, mireu els números al lloc. L’arrodoniment es farà en funció del valor de lloc, de manera que és molt important que recordeu aquest pas o regla.
Al número "813, 265", diguem que voleu arrodonir fins al desè lloc. Això vol dir que heu de fixar-vos en la posició número cent

Pas 4. No canvieu el número si el número del valor del lloc a la dreta és inferior a "5"
Si el dígit més petit després del valor de lloc que voleu arrodonir és inferior a "5" (per exemple, "0", "1", "2", "3" o "4"), deixeu el dígit al valor de referència com és. Això significa que el número al costat del valor de lloc serà "0", de manera que podeu ometre-lo o suprimir-lo al final del número. Aquest procés es coneix com a arrodoniment cap avall.
Per exemple, si voleu arrodonir "0,74" al dècim més proper, mireu el número que hi ha al costat del desè lloc ("4"). Com que "4" és inferior a "5", podeu mantenir o mantenir "7" i eliminar "4" del número de manera que el resultat arrodonit es converteixi en "0, 7"

Pas 5. Augmenteu el número si el número del valor del lloc a la dreta és superior a "5"
Si el dígit més petit després del valor de lloc que voleu arrodonir és superior a "5" (per exemple, "5", "6", "7", "8" o "9"), afegiu "1" al número de el valor de lloc. Com abans, qualsevol altre número a la dreta del dígit o del valor de lloc del punt de referència d'arrodoniment serà "0" perquè es puguin suprimir o ometre. Aquest procés es coneix com a arrodoniment cap amunt.
Per exemple, teniu el número "35". Si voleu arrodonir als deu més propers, observeu el valor de lloc més petit després d'ell ("5"). Per arrodonir un número, afegiu "1" al número del valor de referència (desenes o "3"). Per tant, el resultat d’arrodonir el número “35” al deu més proper és 40
Mètode 2 de 6: arrodoniment de nombres decimals

Pas 1. Determineu el valor de lloc per al punt de referència d'arrodoniment
El vostre professor pot indicar o determinar el valor de lloc si esteu treballant en un problema de matemàtiques. També podeu esbrinar-ho en funció del context i de la sèrie de números utilitzats. Per exemple, quan arrodoneu els diners, és possible que hàgiu d'arrodonir al valor de milers o centenars més proper. Quan arrodoneu el pes d’un objecte, arrodoneu-lo al lloc més proper als quilograms.
- Com menys precisió requereixi, més o més lluny es pot fer l’arrodoniment (fins a un valor de lloc més gran).
- Per obtenir nombres més precisos, cal arrodonir-los al valor de lloc més petit.
- Si heu d’arrodonir una fracció, convertiu-la en un nombre decimal abans d’arrodonir-la.
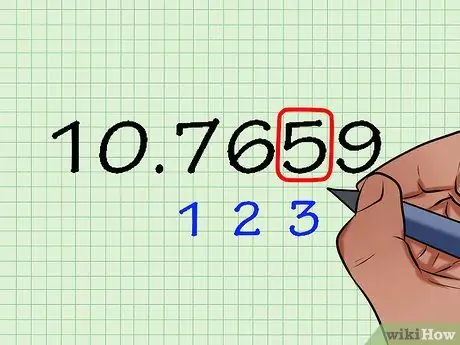
Pas 2. Identifiqueu el valor de lloc que voleu establir com a punt de referència d’arrodoniment
Suposem que teniu el número “10, 7659” i voleu arrodonir-lo al mil·lèsim dígit més proper (“5” al lloc mil·lèsim) o al tercer dígit a la dreta de la coma. També podeu pensar que arrodoneix un nombre a cinc dígits significatius. Per tant, centreu-vos en el número "5" per ara.

Pas 3. Cerqueu el número a la dreta del valor de referència del punt de referència d’arrodoniment
Només cal que observeu un sol dígit a la dreta del valor de referència. A l'exemple anterior, podeu veure el número "9" al costat del número "5". El número "9" determinarà si heu d'arrodonir el número "5" cap amunt o cap avall.

Pas 4. Afegiu-ne un al número del valor de lloc estàndard si el número a la dreta del valor de lloc és "5" (o més)
Aquest procés es coneix com a arrodoniment perquè el nombre del valor de lloc que voleu arrodonir és més gran que el número original. Cal canviar el número "5" que és un número natural a "6". Tots els números a l'esquerra del "5" original es mantindran sense canvis i es poden ometre els números de la part dreta (podeu imaginar-los com a zeros). Per tant, si arrodoneu el número "10.7659" del dígit o número "5", el número s'arrodonirà a "6" de manera que el resultat final de l'arrodoniment sigui "10, 766".
- Tot i que el número "5" se situa entre els números "1" i "9", la gent generalment està d'acord que el número "5" necessita un altre número abans que s'arrodoneixi. Tanmateix, és possible que aquest acord o principi no s'apliqui als professors quan afegeixen notes finals al vostre butlletí.
- Els organismes normatius com el NIST utilitzen un mètode diferent. Quan el número estàndard que cal arrodonir és "5", fixeu-vos en el número de la dreta. Si el número no és "0", arrodoneix-lo. Si el número és "0" o no hi ha cap altre dígit, arrodoneu-lo cap amunt si el dígit estàndard és un número senar, o cap avall si el dígit estàndard és un número parell.

Pas 5. Redoneu el número cap avall si el número de la dreta és inferior a "5"
Si el número situat a la part dreta del valor de referència del punt de referència d’arrodoniment és inferior a “5”, el número del valor de referència de referència continuarà sent el mateix. Tot i que s’anomena arrodoniment cap avall, en aquest procés el número del valor de lloc no canviarà; No es pot canviar per un nombre més petit. Per exemple, si teniu el número "10, 7653", podeu arrodonir-lo a "10, 765" perquè el número "3" al costat de "5" és inferior a "5".
- Si manteniu el número al valor de lloc predeterminat i canvieu els números que hi ha a la dreta a “0”, el resultat final de l’arrodoniment serà inferior al número original. Per tant, es pot dir que el nombre sencer va ser arrodonit cap avall.
- Els dos passos anteriors es representen com a arrodoniment "5/4" a la majoria de calculadores de sobretaula. Normalment, podeu trobar un commutador o un control lliscant que es pugui moure a la posició d'arrodoniment "5/4" per obtenir el resultat d'arrodoniment.
Mètode 3 de 6: arrodoniment de nombres (enter)
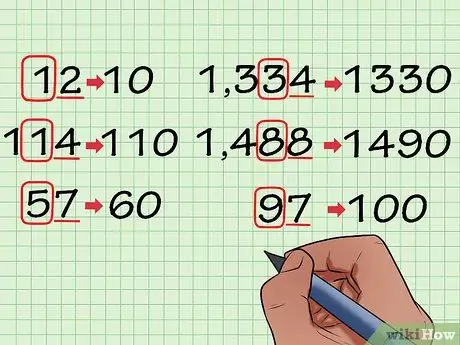
Pas 1. Arrodoneix un número al dígit o al lloc de desenes més proper
Per fer-ho, observeu el número a la dreta del dígit de les desenes (el valor de lloc del punt de referència d’arrodoniment). Els dígits o les desenes són el segon dígit de l'últim dígit, abans dels dígits (al número "12", per exemple, el valor de lloc de les unitats està ocupat pel número "2"). Si el número de la unitat és inferior a "5", mantingueu el número en el valor de lloc estàndard. Si el número és superior o igual a "5", afegiu "1" al número del valor de lloc estàndard. Aquests són alguns exemples que podeu estudiar:
- ”12” “10”
- ”114” “110”
- ”57” “60”
- ”1.334” “1.330”
- ”1.488” “1.490”
- ”97” “100”

Pas 2. Redoneu el número al dígit més proper o al lloc de centenars
Seguiu les mateixes regles per arrodonir els números al centenari o al lloc més propers. Observeu el valor de lloc de centenars (el tercer de l'últim dígit), just a l'esquerra del dígit de les desenes. Per exemple, al número "1.234", el número "2" és el dígit de centenars) Després, utilitzeu el número de la part dreta (el dígit de les desenes) per comprovar si heu d'arrodonir cap amunt o cap avall i, a continuació, feu el següent números “0”. Aquests són alguns exemples que podeu estudiar:
- ”7.891” -- > “7.900”
- ”15.753” “15.800”
- ”99.961” “100.000”
- ”3.350” “3.400”
- ”450” “500”

Pas 3. Redoneu el número al dígit més proper o al lloc de milers
Les mateixes regles s'apliquen a preguntes com aquesta. Només cal saber reconèixer els dígits o el valor de lloc de milers, que és el quart número de la dreta. Després d'això, comproveu el número del dígit o del lloc dels centenars (a la dreta del dígit dels milers). Si el nombre de dígits de centenars és inferior a "5", arrodoneix cap avall. Si el nombre és superior o igual a "5", arrodoneu-lo cap amunt. Aquests són alguns exemples que podeu estudiar:
- ”8.800” “9.000”
- ”1.015” “1.000”
- ”12.450” “12.000”
- ”333.878” “334.000”
- ”400.400” “400.000”
Mètode 4 de 6: arrodoniment de nombres a dígits significatius

Pas 1. Comprendre els dígits significatius
Podeu pensar en dígits significatius com a dígits "interessants" o "significatius" que us proporcionen informació útil sobre un número. Això vol dir que es poden ignorar tots els zeros de la part dreta del enter o del costat esquerre del decimal perquè els zeros només serveixen com a "omplert de lloc". Per trobar el nombre de dígits significatius en un número, només cal comptar el nombre de dígits d’esquerra a dreta. Aquests són alguns exemples:
- "1, 239" té 4 dígits significatius.
- "134, 9" té 4 dígits significatius.
- "0,0165" té 3 dígits significatius.

Pas 2. Redoneu el número a un nombre de dígits significatius
El nombre de dígits dependrà del problema en què estigueu treballant. Si se us demana que arrodoneu un número a dos dígits significatius, per exemple, haureu d’identificar el segon dígit significatiu i mirar el número que hi ha a la dreta per veure si cal arrodonir-lo cap amunt o cap avall. Aquests són alguns exemples:
- "1, 239" es pot arrodonir fins a 3 dígits significatius a "1, 24". Això es deu al fet que el tercer dígit significatiu és "3" i el número a la dreta és "9". El número "9" és superior a "5", de manera que l'arrodoniment es fa cap amunt.
- "134, 9" es pot arrodonir a 1 dígit significatiu a "100". Això es deu al fet que el primer dígit significatiu és "1" i el número a la dreta és "3". El número "3" és més petit que "5", de manera que l'arrodoniment es fa cap avall.
- "0,0165" es pot arrodonir fins a 2 dígits significatius a "0,017". Això es deu al fet que el segon dígit significatiu és "6" i el número a la dreta és "5", de manera que cal arrodonir-lo.

Pas 3. Redoneu la suma al nombre adequat de dígits significatius
Per fer arrodoniments, primer heu de sumar els números del problema. Després d'això, busqueu el nombre amb el menor nombre de dígits significatius i arrodoneu la suma a aquest nombre. A continuació s’explica com:
- ”13, 214” + 234, 6 + 7, 0350 + 6, 38 = 261.2290”
- El segon número del problema d'addició ("234, 6") té una precisió de fins a una desena part, de manera que té quatre dígits significatius.
- Arrodoneix la suma de manera que només tingui dècimes dígits. Per tant, "261, 2290" es pot arrodonir a "261, 2".

Pas 4. Arrodoneix el resultat de la multiplicació al nombre adequat de dígits significatius
En primer lloc, multipliqueu tots els números del problema. Després d'això, comproveu el nombre que s'ha d'arrodonir al menor nombre de dígits significatius. Finalment, arrodoneu el resultat de la multiplicació final per ajustar el nivell de precisió del nombre. A continuació s’explica com:
- ”16, 235 × 0.217 × 5 = 17, 614975”
- Recordeu que "5" és l'únic número que té un dígit significatiu. Això significa que la resposta de multiplicació final només pot tenir un dígit significatiu.
- "17, 614975" es pot arrodonir a un dígit significatiu a "20".
Mètode 5 de 6: utilitzar la calculadora

Pas 1. Seleccioneu la funció "rodona" a la calculadora
Si feu servir la calculadora TI-84, feu clic al botó Matemàtiques i, a continuació, canvieu a l'opció "NUM". Moveu la selecció a la funció "rodona" i, a continuació, premeu el botó "D'acord".
Les calculadores de TI més antigues poden tenir funcions o menús lleugerament diferents

Pas 2. Introduïu el número que voleu arrodonir
El camp de diàleg mostrarà la funció o el codi "rodona". Utilitzeu les tecles de la calculadora per introduir el número que heu d'arrodonir, però no premeu "Retorn" immediatament després.
Si heu d’arrodonir una fracció, convertiu-la primer en un nombre decimal

Pas 3. Introduïu una coma i, a continuació, introduïu el nombre de decimals que voleu establir el límit o límit d'arrodoniment
Després d’introduir el número que voleu arrodonir, cerqueu i premeu el botó de coma de la calculadora després. A continuació, introduïu el nombre de decimals que necessiteu per establir el límit d'arrodoniment.
- Per exemple, a la pantalla de la calculadora podeu veure un número com aquest: round (6234, 1).
- Per a les calculadores amb format indonesi, la visualització de codis o números a la calculadora pot tenir aquest aspecte: rodó (6, 234, 1).
- Si no especifiqueu el nombre de posicions decimals, obtindreu un codi o una fracció d'error molt estrany.

Pas 4. Acabeu amb claudàtors i premeu la tecla "Retorn"
Després d'especificar el nombre de posicions decimals, introduïu el parèntesi de tancament a l'equació i premeu la tecla "Retorn". La calculadora mostrarà el número que s’ha arrodonit al punt decimal o punt decimal que especifiqueu.
Mètode 6 de 6: arrodoniment de números a Microsoft Excel
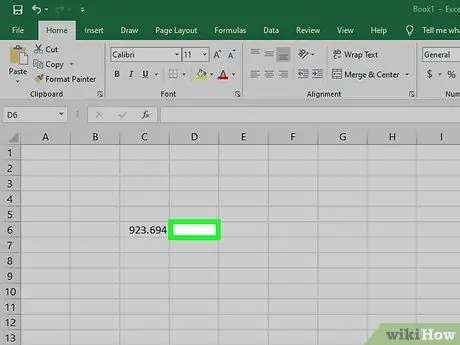
Pas 1. Feu clic al quadre situat al costat del número que voleu arrodonir
Introduïu totes les dades i assegureu-vos que les introduïu correctament. Feu clic al cursor al quadre situat al costat del número que heu d'arrodonir (sempre que el quadre estigui buit).
Al quadre on feu clic es mostrarà el número arrodonit
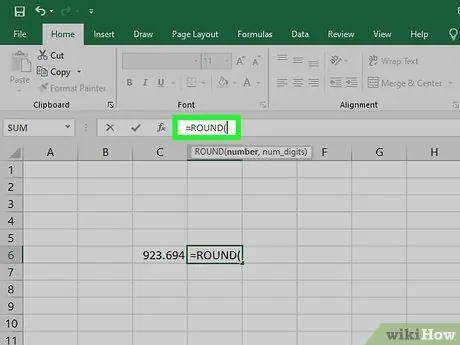
Pas 2. Escriviu la fórmula "= ROUND (" al camp de l'equació
Al camp "fx" a la part superior de la pantalla, escriviu un signe d'igualtat i la paraula "RODÓ", seguit d'un parèntesi d'obertura. La fórmula de l’equació es formarà de manera que hi pugueu introduir dades.
La fórmula és molt senzilla, però assegureu-vos que no oblideu cap element ni puntuació
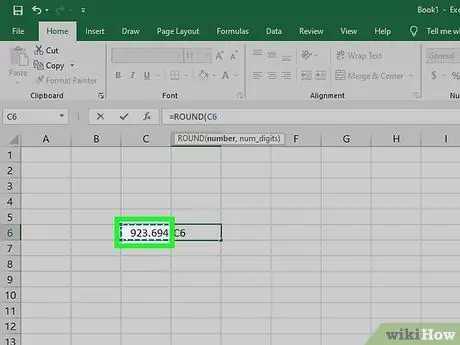
Pas 3. Feu clic al quadrat amb el número que voleu arrodonir
Es marcaran els quadrats i s'introduiran els números a l'equació. Les lletres quadrades i els números que contenen les dades (en aquest cas, el nombre que cal arrodonir) es mostraran a la columna "fx".
Per exemple, si feu clic al quadre "A1", la columna "fx" mostrarà la fórmula següent: "= ROUND (A1
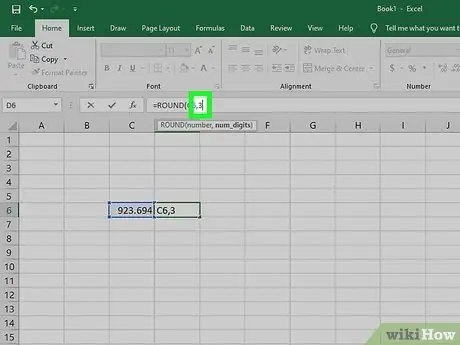
Pas 4. Escriviu una coma i introduïu el nombre de dígits que voleu establir com a límit d'arrodoniment
Per exemple, si voleu que el número del quadre "A1" s'arrodoneixi a tres decimals, escriviu ", 3" a la columna. Si voleu arrodonir les dades al nombre enter més proper, escriviu “0”.
Si voleu arrodonir a la següent multiplicació de "10", utilitzeu "-1"
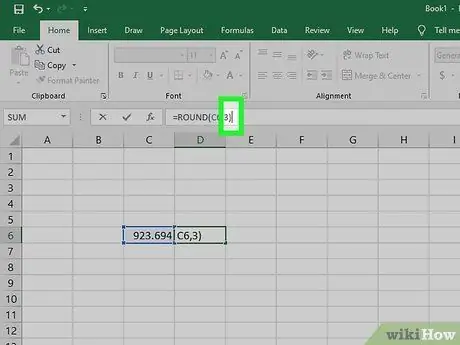
Pas 5. Acabeu amb claudàtors i premeu la tecla "Retorn"
Per resoldre l’equació, escriviu un parèntesi de tancament per fer saber a Excel que heu acabat d’introduir la fórmula. Premeu la tecla "Retorn" perquè l'Excel pugui arrodonir el número que heu introduït.
La vostra resposta es mostrarà al quadre on heu fet clic
Consells
- Després de conèixer el valor de lloc que s'utilitzarà com a punt de referència d'arrodoniment, subratlleu el número del valor de lloc. D'aquesta manera, no us confondreu quan cerqueu el dígit de referència d'arrodoniment i el dígit del costat dret (el número que determina el tipus d'arrodoniment que cal fer).
- Podeu accedir gratuïtament a diverses calculadores d’arrodoniment en línia.






