IQR és l'interval interquartil o l'interval d'arrel quartil d'un conjunt de dades. IQR s’utilitza en anàlisis estadístiques per ajudar a treure conclusions sobre un conjunt de dades. IQR s’utilitza més sovint que l’interval perquè IQR no inclou les dades més externes. Continueu llegint per aprendre a trobar l'IQR.
Pas
Mètode 1 de 3: comprensió de la QI
Pas 1. Entendre com utilitzar IQR
Bàsicament, IQR és una manera d’entendre la difusió d’un conjunt de nombres. El rang del quartil arrel es defineix com la diferència entre el quartil superior (25% superior) i el quartil inferior (25% més baix) del conjunt de dades.
Consell:
El quartil inferior normalment s’escriu com a Q1 i el quartil superior s’escriu com a Q3, cosa que fa que el punt mitjà de les dades sigui Q2 i el punt més alt sigui Q4.
Pas 2. Comprendre els quartils
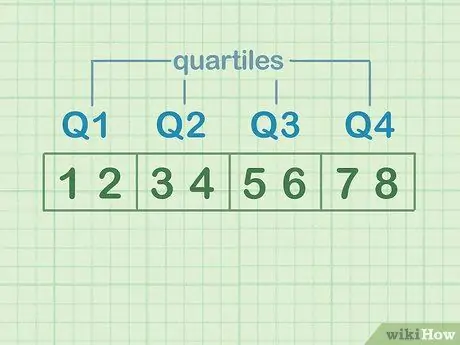
Per il·lustrar quartils, divideix el conjunt de nombres en quatre parts iguals. Cadascuna d'aquestes parts és un "quartil". Suposem que els conjunts de dades són: 1, 2, 3, 4, 5, 6, 7, 8.
- 1 i 2 són el primer quartil o Q1
- 3 i 4 són el segon quartil o Q2
- 5 i 6 són el tercer quartil o Q3
- 7 i 8 són el quart quartil o Q4
Pas 3. Apreneu la fórmula
Per trobar la diferència entre els quartils superior i inferior, heu de restar el percentil 75 del percentil 25.
La fórmula està escrita: Q3 - Q1 = IQR
Mètode 2 de 3: compilació del conjunt de dades
Pas 1. Recopileu les vostres dades
Si estudieu IQR a classe i en proves, se us pot proporcionar un conjunt de dades ja preparades, per exemple 1, 4, 5, 7, 10. Aquest és el vostre conjunt de dades: els números amb els quals treballareu. Tanmateix, podeu crear els vostres propis números a partir de preguntes de taula o problemes relacionats amb la història.
Assegureu-vos que cada número representi el mateix:
per exemple, el nombre d’ous a cada niu d’una població d’ocells definida o el nombre de places d’aparcament ubicades a cada casa d’un bloc especificat.
Pas 2. Ordeneu les dades en ordre ascendent
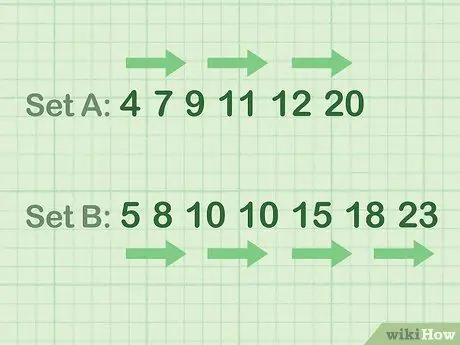
En altres paraules: organitzeu els números del més petit al més gran. Utilitzeu els consells dels exemples següents.
- Exemple de dades de nombres parells (conjunt A): 4 7 9 11 12 20
- Exemple de dades de nombres senars (conjunt B): 5 8 10 10 15 18 23
Pas 3. Dividiu les dades en dos
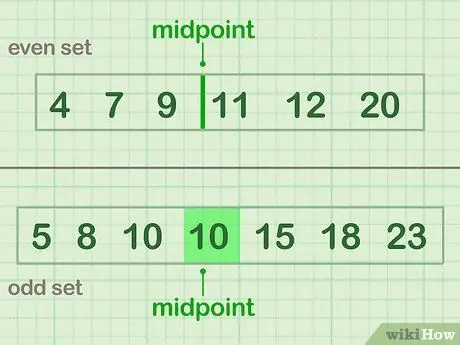
Per dividir-vos per la meitat, cerqueu el punt mitjà de les vostres dades: el nombre o els números que es troben al centre del conjunt de dades. Si teniu un nombre senar de dades, trieu el número que hi ha al centre. Si teniu un nombre parell de dades, el punt mitjà es troba entre els dos nombres més mitjans.
- Un exemple parell (conjunt A) que té un punt mig entre 9 i 11: 4 7 9 | 11 12 20
- Un exemple estrany (conjunt B) que té un punt mitjà de valor (10): 5 8 10 (10) 15 18 23
Mètode 3 de 3: càlcul de la QII
Pas 1. Cerqueu la mediana de la meitat inferior i superior de les dades
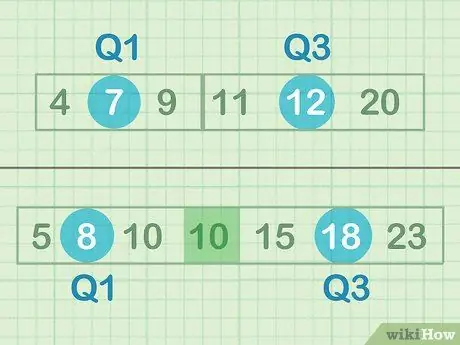
La mediana és el "punt mig" o número que es troba al mig d'un conjunt de nombres. En aquest cas, no busqueu el punt mitjà de tots els números, sinó que busqueu el punt mitjà relatiu dels subconjunts de dades superiors i inferiors. Si teniu un nombre senar de dades, no incloeu el número mitjà; per exemple, al conjunt B, no cal que inclogueu ni un sol 10.
-
Exemple parell (conjunt A):
- Mitjana de la meitat inferior de les dades = 7 (Q1)
- Mitjana de la meitat superior de les dades = 12 (Q3)
-
Exemple estrany (conjunt B):
- Mitjana de la meitat inferior de les dades = 8 (Q1)
- Mitjana de la meitat superior de les dades = 18 (Q3)
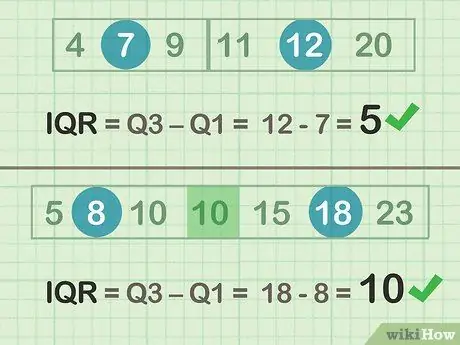
Pas 2. Resteu Q3-Q1 per determinar el QIQ
Ara ja sabeu quantes xifres es troben entre els percentils 25 i 75. Podeu utilitzar aquest número per entendre la difusió de les dades. Per exemple, si una prova té una puntuació màxima de 100 i l’IQR de la puntuació és 5, podeu suposar que la majoria de les persones que fan la prova tenen gairebé la mateixa comprensió perquè l’interval d’alts i mínims no és molt gran. Tanmateix, si el coeficient intel·lectual de puntuació de la prova és 30, potser us comenceu a preguntar per què algunes persones obtenen una puntuació tan alta i d’altres tan baixes.
- Exemple parell (conjunt A): 12 -7 = 5
- Exemple estrany (conjunt B): 18 - 8 = 10
Consells
És important aprendre a fer-ho tot sol. Tot i això, hi ha diverses calculadores IQR en línia que podeu utilitzar per comprovar el vostre treball. No confieu massa en les aplicacions de calculadores si apreneu això a classe. Si se us demana que busqueu l'IQR en una prova, haureu de saber com trobar-lo manualment
WikiHow relacionat
- Com detectar valors atípics
- Com es calcula l'abast d'un conjunt de dades
- Com fer un quadre i un diagrama de tenda
