- Autora Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:12.
- Última modificació 2025-01-23 12:08.
El desplaçament en física denota un canvi en la posició d’un objecte. Quan es calcula el desplaçament, es calcula la distància que té un objecte en funció de la seva ubicació inicial i final. La fórmula que utilitzeu per calcular el desplaçament depèn de la variable donada al problema. Seguiu aquests passos per calcular el desplaçament.
Pas
Part 1 de 5: càlcul del desplaçament resultant

Pas 1. Utilitzeu la fórmula del desplaçament resultant si s'utilitza la unitat de distància per indicar la vostra ubicació inicial i final
Tot i que la distància és diferent del desplaçament, el problema de desplaçament resultant busca quants quilòmetres o metres ha recorregut l'objecte. Utilitzarà aquesta unitat de mesura per calcular el desplaçament i la distància amb què es desvia la ubicació d’un objecte del seu punt de partida.
- La fórmula del desplaçament resultant s’escriu com: S = x² + y². S és el desplaçament. X és la primera direcció de moviment de l'objecte i Y és la segona direcció de moviment de l'objecte. Si el vostre objecte només es mou en una direcció, llavors Y = 0.
- Un objecte només es pot moure en un màxim de dues direccions perquè moure’s al llarg d’un eix nord / sud o est / oest es considera moviment neutre.

Pas 2. Connecteu els punts per ordre de moviment i etiqueteu-los des de la A-Z
Utilitzeu una regla per dibuixar una línia recta d’un punt a un altre.
- Recordeu també de connectar el punt de partida amb el punt final mitjançant una línia recta. Aquest és el desplaçament que calcularem.
- Per exemple, si un objecte es mou cap a l'est 300 m i cap al nord 400 m, formarà un triangle rectangle. AB serà el primer tram del triangle i BC serà el segon tram. AC serà la hipotenusa del triangle i la seva magnitud és el desplaçament de l'objecte. En aquest exemple, les dues direccions són est i nord.

Pas 3. Introduïu els valors de x² i y²
Ara que ja coneixeu les dues direccions de moviment de l'objecte, introduïu els valors a les variables adequades.
Per exemple, x = 300 i y = 400. La vostra fórmula hauria de tenir aquest aspecte: S = 300² + 400²
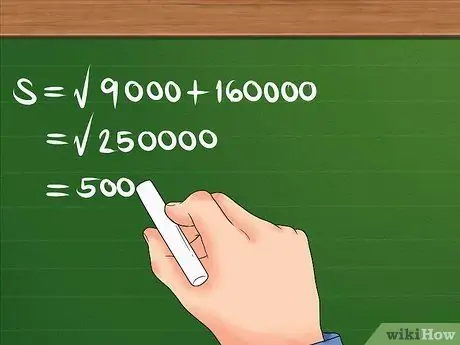
Pas 4. Calculeu la fórmula utilitzant l'ordre de les operacions
Primer, quadrats 300 i 400, després sumeu-los i trobeu l’arrel quadrada de la suma.
Per exemple: S = 90000 + 160000. S = 250000. S = 500. Ara ja saps que el desplaçament és de 500 m
Part 2 de 5: quan es coneixen la velocitat i el temps

Pas 1. Utilitzeu aquesta fórmula quan el problema us indiqui la velocitat d’un objecte i el temps que triga
Alguns problemes matemàtics no us indiquen fins a quin punt o amb quina velocitat es mou un objecte. Podeu calcular el desplaçament utilitzant aquesta magnitud de temps i velocitat.
-
En aquest cas, la fórmula es converteix en: S = 1/2 (u + v) t.
U = velocitat inicial de l'objecte o la velocitat amb què l'objecte comença a moure's en una direcció determinada. V = la velocitat final de l'objecte o la velocitat amb què l'objecte es mou cap a la seva ubicació final. T = el temps que triga l'objecte a arribar a la seva ubicació final.
- Exemple: un cotxe baixa per la carretera durant 45 segons (temps necessari). El cotxe gira a l’oest a 20 m / s (velocitat inicial) i al final de la carretera, la seva velocitat és de 23 m / s (velocitat final). Calculeu el desplaçament a partir d’aquests factors.

Pas 2. Introduïu la velocitat i el temps requerits a les variables adequades
Ara que ja sabeu fins a quin punt es mou el cotxe, a quina velocitat es mou al principi i al final, podeu trobar la distància des de la ubicació inicial fins a la ubicació final.
La fórmula hauria de ser així: S = 1/2 (20 + 23) 45

Pas 3. Calculeu la fórmula després de col·locar els valors al lloc correcte
Recordeu que heu de seguir l'ordre de les operacions, en cas contrari els desplaçaments donaran lloc a valors molt diferents.
- Per a aquesta fórmula, no importa si canvieu accidentalment les velocitats inicial i final. Com que primer sumareu aquests números, no importa on estiguin entre parèntesis. No obstant això, per a altres fórmules, canviar les velocitats inicial i final donarà lloc a diferents valors de desplaçament.
- La vostra fórmula hauria de ser així: S = 1/2 (43) 45. Primer divideix 43 per 2, el que resulta en 21, 5. Després multiplica 21, 5 per 45, de manera que el resultat és de 967,5 metres. 967, 5 és la magnitud del vostre desplaçament o fins a quin punt s’ha desplaçat el vostre cotxe des del punt de partida.
Part 3 de 5: quan es coneixen la velocitat inicial, l’acceleració i el temps
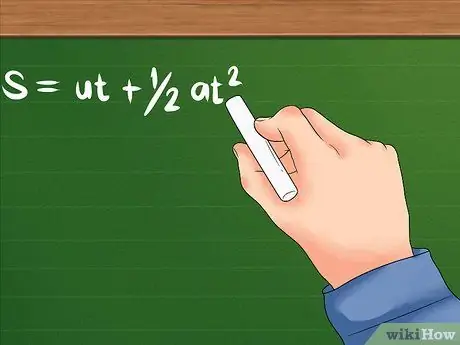
Pas 1. Utilitzeu la fórmula modificada quan es conegui l’acceleració a més de la velocitat i el temps inicials
Algunes preguntes només us indicaran la rapidesa amb què es mou l’objecte al principi, la rapidesa amb què l’objecte comença a accelerar-se i fins a quin punt es mou l’objecte. Necessitareu la següent fórmula.
- La fórmula d’aquest problema és: S = ut + 1 / 2at². U encara indica la velocitat inicial; a és l’acceleració de l’objecte o la velocitat amb què comença a canviar la seva velocitat. T pot significar el temps que triga o una determinada quantitat de temps que un objecte triga a accelerar. Tots dos utilitzaran unitats de temps com ara segons, hores i altres.
- Suposem que un cotxe que es mou a 25 m / s (velocitat inicial) comença a accelerar a 3 m / s2 (acceleració) durant 4 segons (temps). Quin és el desplaçament del cotxe al cap de 4 segons?

Pas 2. Introduïu els valors a la fórmula
A diferència de la fórmula anterior, aquí només es representa la velocitat inicial, així que assegureu-vos d’introduir les dades correctes.
Basant-se en les dades de mostra anteriors, la vostra fórmula seria així: S = 25 (4) + 1/2 (3) 4². Ajuda a afegir parèntesis al voltant de la magnitud i el temps de l’acceleració per ajudar-vos a separar els números
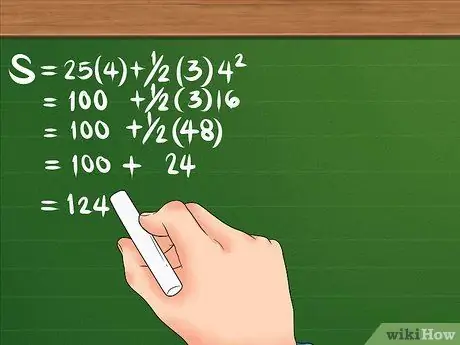
Pas 3. Calculeu el desplaçament fent-lo en l'ordre correcte de les operacions
Una manera ràpida d’ajudar-vos a recordar la seqüència d’operacions és el pont del ruc Kur ir Kua ci Kadang Ba wa Juragan Turtles. Això representa l'ordre correcte: parèntesis, quadrats, multiplicació, divisió, suma i resta.
Vegem de nou la fórmula: S = 25 (4) + 1/2 (3) 4². Primer, quadrat 4, el resultat és 16. Després, multiplica 16 per 3, fent 48; llavors també multiplica 25 per 4, per fer 100. Divideix 48 per 2, per fer 24. La teva equació hauria de ser així: S = 100 + 24. Un cop sumats els dos junts, el desplaçament és de 124 metres
Part 4 de 5: càlcul del desplaçament angular

Pas 1. Cerqueu el desplaçament angular a mesura que l'objecte es mou en un camí circular
Tot i que continuareu calculant el desplaçament mitjançant una línia recta, haureu de trobar la diferència entre les ubicacions inicials i finals de l'objecte a mesura que es mou en un camí circular.
- Imagineu-vos una noia asseguda en un carrusel. Mentre gira amb el carrusel, es mourà per un camí circular. El desplaçament angular intenta trobar la distància més curta entre la ubicació inicial i la final quan l’objecte no es mou en línia recta.
- La fórmula del desplaçament angular és: = S / r, on S és el desplaçament lineal, r és el radi i és el desplaçament angular. El desplaçament lineal és fins a quin punt es mou un objecte al llarg d’un arc. El radi és la distància de l'objecte al centre del cercle. El desplaçament angular és el valor que volem trobar.

Pas 2. Connecteu el desplaçament lineal i el radi a l'equació
Recordeu que el radi és la distància del centre del cercle; alguns problemes us indicaran el diàmetre d’un cercle, que s’ha de dividir per 2 per trobar el radi.
- Heus aquí un exemple de problema: una noia munta un carrusel. El seient es troba a 1 metre del centre del cercle (el radi). Si la noia es mou en una trajectòria d'arc d'1,5 metres (desplaçament lineal), quin és el seu desplaçament angular?
- La vostra equació serà així: = 1,5 / 1.
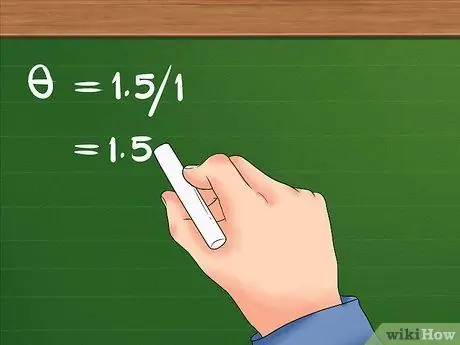
Pas 3. Divideix el desplaçament lineal pel radi
Aquesta divisió donarà lloc al desplaçament angular de l'objecte.
- Després de dividir 1,5 per 1, el resultat és 1,5 i el desplaçament angular de la noia és 1,5 radians.
- Com que el desplaçament angular mesura quant gira un objecte des de la seva posició inicial, s’hauria de mesurar com un angle, no com una distància. El radian és la unitat que s’utilitza per mesurar angles.
Part 5 de 5: Descripció de la migració
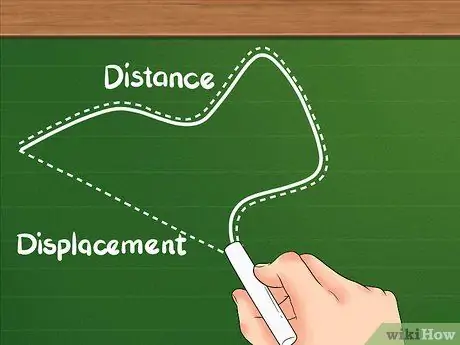
Pas 1. Sabeu que la distància té una definició diferent de la de desplaçament
La distància mostra fins a quin punt la distància total recorreguda per l’objecte.
- La distància es coneix sovint com una quantitat escalar. La distància mostra la distància recorreguda per un objecte independentment de la direcció de l’objecte.
- Per exemple, si camineu 2 passos cap a l'est, 2 passos cap al sud, 2 passos cap a l'oest i, a continuació, 2 passos cap al nord, tornareu a la vostra posició inicial. Tot i que heu passat pel total distància A 10 passos, només moure A 0 passos perquè la vostra ubicació final és la mateixa que la vostra ubicació inicial (el vostre camí s’assembla a un quadre).

Pas 2. Compreneu que el desplaçament és la diferència entre dues ubicacions
El desplaçament no és la suma total del moviment com la distància; els canvis es centren en l'àrea entre les ubicacions inicials i finals.
- El desplaçament s’anomena quantitat vectorial i mostra el canvi en la posició d’un objecte tenint en compte la direcció de moviment de l’objecte.
- Per exemple, camineu cap a l’est durant 5 passos. Si torneu cap a l'oest 5 passos, us mourà en la direcció oposada de la vostra ubicació original. Tot i que heu recorregut deu passos, la vostra posició no ha canviat; el vostre desplaçament és de 0 passos.

Pas 3. Recordeu les paraules cap endavant i cap enrere quan intenteu imaginar el desplaçament
Moure’s en direcció contrària elimina el desplaçament d’un objecte.
Imagineu-vos un entrenador de futbol endavant i enrere al marge. Mentre cridava als jugadors, va canviar d’esquerra a dreta diverses vegades. Si el veieu com es mou d’esquerra a dreta, observeu la distància total que ha recorregut. Tot i així, suposem que l’entrenador s’atura per parlar amb el quarterback al marge. Si es troba en un punt diferent de la seva ubicació inicial abans de moure’s, aleshores observeu el moviment de l’entrenador

Pas 4. Sabeu que el desplaçament es mesura mitjançant un camí recte, no un camí circular
Per trobar el desplaçament, heu de trobar la forma més curta i eficient de calcular la diferència entre dos punts.
- Un camí circular us portarà des de la vostra ubicació inicial fins a la vostra ubicació final, però no és el camí més curt. Per ajudar-vos a visualitzar-lo, imagineu-vos que camineu en línia recta i us trobeu amb un pilar. No es pot trencar aquest pilar i, per tant, el voreja. Tot i que la vostra posició final és la mateixa que si heu obert el pilar, necessitareu passos addicionals per assolir aquest objectiu.
- Tot i que el desplaçament representa un camí recte, sàpiga que podeu mesurar el desplaçament d’un objecte que és actualment moure’s per un camí circular. Aquest desplaçament s’anomena desplaçament angular i es pot calcular trobant el camí més curt des de la ubicació inicial fins a la ubicació final.

Pas 5. Sabeu que el desplaçament pot ser negatiu, a diferència de la distància
Si s’arriba a la ubicació final movent-se en la direcció oposada a la direcció inicial, el desplaçament és negatiu.
- Per exemple, caminem 5 passos cap a l'est i després 3 passos cap a l'oest. Tot i que, per càlcul, es mou dos passos de la ubicació inicial, el desplaçament és -2 perquè es mou en la direcció oposada. La vostra distància sempre serà positiva perquè no podeu comptar cap enrere en passos, quilòmetres, etc.
- El desplaçament negatiu no significa que disminueixi el desplaçament. Negatiu significa que la direcció és contrària.

Pas 6. Adonar-se que de vegades la distància i el desplaçament poden ser els mateixos
Si camineu recte durant 25 graons i us atureu, la distància que recorrereu serà igual al desplaçament respecte a la vostra ubicació original.
- Això només s’aplica quan es desplaça des d’una ubicació des de la ubicació inicial en línia recta. Per exemple, viviu a San Francisco, Califòrnia, i obteniu una nova feina a Las Vegas, Nevada. Cal anar a Las Vegas per estar a prop de la seva feina. Si puja a un avió que vola recte de San Francisco a Las Vegas, recorrerà la mateixa distància i desplaçament x.
- Tanmateix, si conduïu de San Francisco a Las Vegas, recorrereu una distància x, però una distància y. Com que conduir un cotxe sol tenir direccions variables (a l’est d’aquesta carretera, a l’oest d’aquesta carretera), recorrereu distàncies més llargues que la distància més curta entre les dues ciutats.






