- Autora Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 11:00.
- Última modificació 2025-01-23 12:10.
Hi ha moltes formes diferents de formes planes i hi ha moltes raons per les quals és possible que vulgueu calcular la superfície: des de fer deures fins a calcular quanta pintura es necessita per repintar una sala d’estar. No us preocupeu, wikiHow té la resposta! Comenceu pel pas 1 següent per saber calcular l'àrea d'una figura plana.
Pas
Mètode 1 de 7: quadrat, rectangle i paral·lelograma
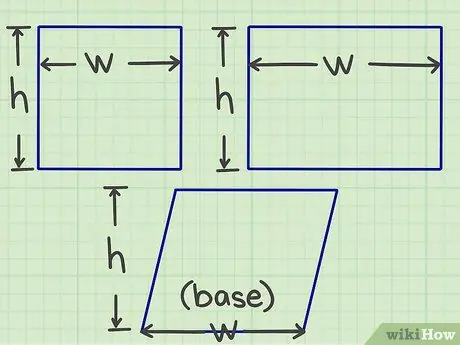
Pas 1. Mesureu la longitud i l'amplada
Comenceu a mesurar o esbrinar la longitud i l'amplada de la forma plana (o dit d'una altra manera, la mida de cadascun dels dos costats que es troben en un punt).
- Per a un paral·lelogram, heu de trobar la base i l'alçada, però, en termes senzills, la idea és la mateixa que la longitud i l'amplada.
- Al món real, és possible que hàgiu de mesurar-lo vosaltres mateixos, però a l’hora de fer els deures, el professor normalment ja ha escrit els números juntament amb una imatge de la forma.
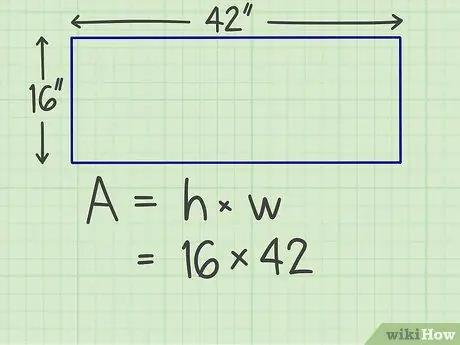
Pas 2. Multipliqueu els costats
Multiplicar un costat per l'altre. Per exemple, suposem que teniu un rectangle amb una amplada de 16 polzades i una longitud de 42 polzades, de manera que heu de calcular 16 x 42.
Si calculeu l'àrea d'un quadrat (abans quadrat), estalvieu temps quadrant un dels seus costats amb una calculadora. Si el costat mesura 4 m, premeu la tecla 4 i, a continuació, premeu la tecla quadrada de la calculadora per mostrar el resultat. Quadrat significa multiplicar un nombre per si mateix
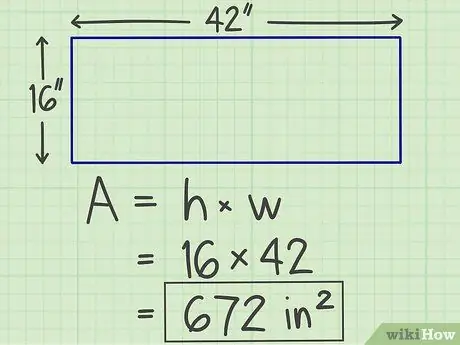
Pas 3. Escriviu els resultats
La multiplicació que vau fer anteriorment produirà un nombre, que és l'àrea del pla que esteu calculant, amb la unitat "quadrat". Per tant, el rectangle que hem calculat anteriorment té una àrea de 672 polzades quadrades.
De vegades, aquesta unitat quadrada també s’escriu com un petit 2 que puja lleugerament després del nom de la unitat (com els poders d’escriptura)
Mètode 2 de 7: Trapezoide
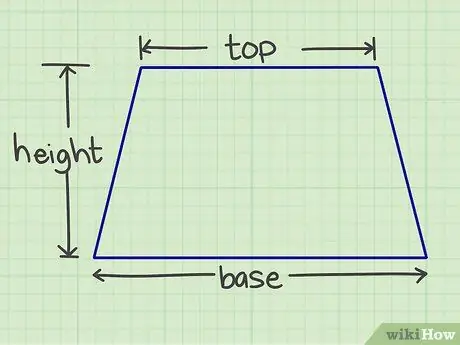
Pas 1. Mesureu el nombre requerit
Haureu de mesurar la base, el sostre i l’alçada. La base i el sostre són laterals paral·lels, mentre que l’alçada és una línia perpendicular que connecta els dos costats paral·lels.
Al món real, és possible que hàgiu de mesurar-lo vosaltres mateixos, però a l’hora de fer els deures, el professor normalment ja ha escrit els números juntament amb una imatge de la forma
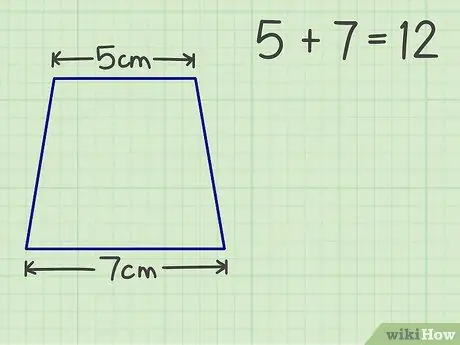
Pas 2. Sumeu els dos costats paral·lels
Per exemple, el nostre trapezi té un sostre de 5 cm i una base de 7 cm. La suma dels dos costats paral·lels és 12.
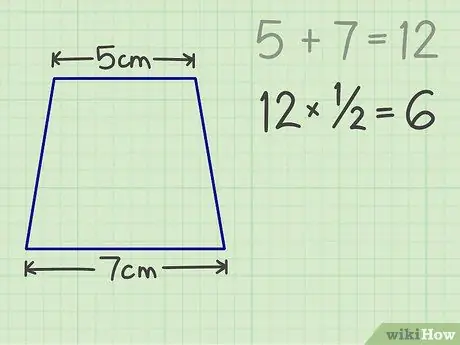
Pas 3. Multiplicar el nombre per 1/2, el resultat és 6
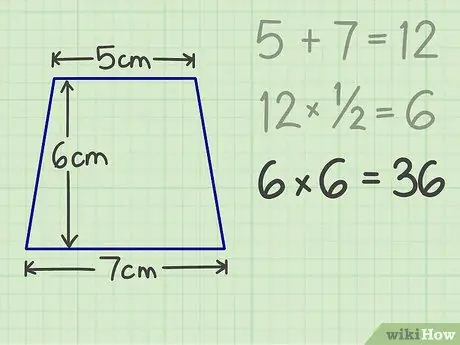
Pas 4. Després d'això, multipliqueu el resultat per l'alçada
Per exemple, si un trapezi té una alçada de 6 cm, el resultat final serà de 36.
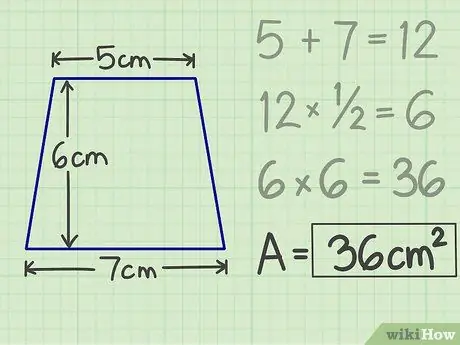
Pas 5. Escriviu els resultats
La multiplicació que vau fer anteriorment produirà un nombre, és a dir, l'àrea del trapezoide. Així doncs, per a un trapezi amb un sostre de 5 cm, una base de 7 cm i una alçada de 6 cm, la superfície és de 36 cm quadrats.
Mètode 3 de 7: Cercle
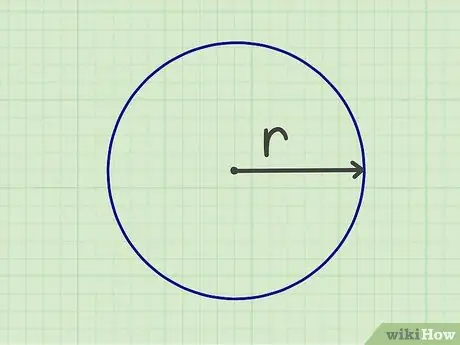
Pas 1. Mesureu el radi
Per poder calcular l'àrea d'un cercle, heu de mesurar el radi. el radi és la distància des del centre del cercle fins a la seva vora. També podeu mesurar el radi mesurant el diàmetre (l’amplada del cercle de vora a cant), dividint el nombre per dos.
Al món real, és possible que hàgiu de mesurar-lo vosaltres mateixos, però a l’hora de fer els deures, el professor normalment ja ha escrit els números juntament amb una imatge de la forma
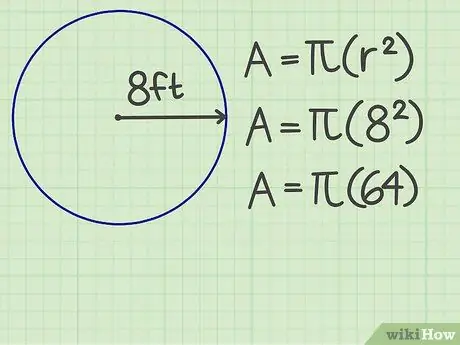
Pas 2. Quadra els dits
Multiplicar el nombre de radis per si mateix. Per exemple, el radi d’un cercle és de 8 peus, de manera que el resultat és 64.
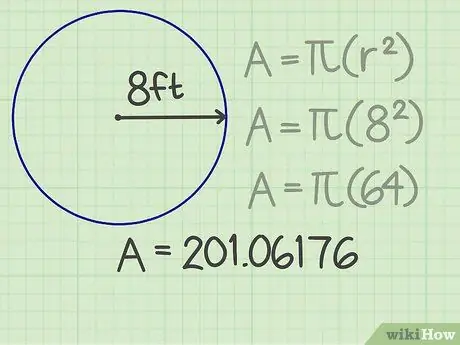
Pas 3. Multiplicar el resultat per pi
Pi (π) és un nombre important utilitzat en diverses fórmules. Si utilitzeu una calculadora, premeu la tecla pi per obtenir resultats realment precisos. En cas contrari, per facilitar els càlculs, podeu arrodonir pi a uns quants dígits després de la coma, per exemple, 3, 14159. Quan multipliqueu aquest nombre pel quadrat del radi, el resultat és 201, 06176.
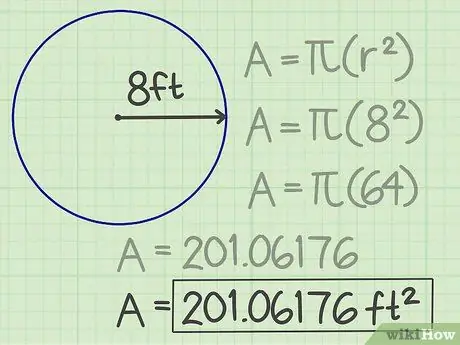
Pas 4. Escriviu els resultats
El nombre obtingut, 201, 06176 és l'àrea del cercle. Així, la seva superfície és de 201.06176 peus quadrats.
Mètode 4 de 7: sector (Juring)
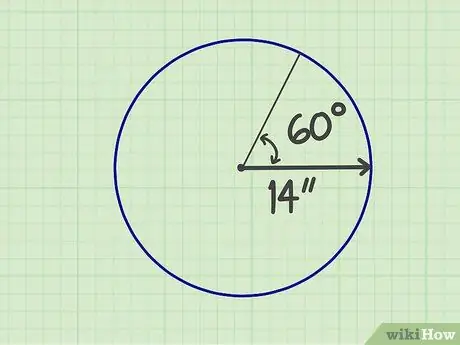
Pas 1. Mesureu els números necessaris
Un sector és una secció d’un cercle format per dos radis i una vora, de manera que la forma és com un ventall. Cal conèixer la mida del radi i l’angle que conforma el “ventilador”. Per exemple, suposem que un sector té un radi de 14 polzades i un angle de 60 graus.
Al món real, és possible que hàgiu de mesurar-lo vosaltres mateixos, però a l’hora de fer deures, el professor ja sol escriure els números juntament amb una imatge de la forma
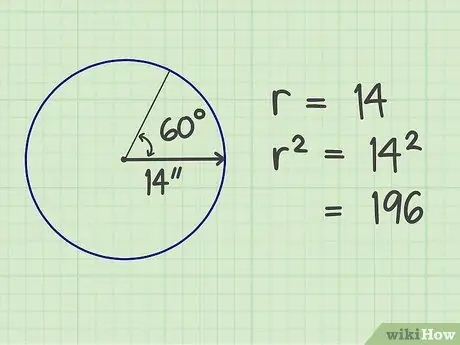
Pas 2. Quadra els dits
Multiplicar el nombre de radis per si mateix. El resultat és 196 (14x14).

Pas 3. Multiplicar el resultat per pi
Pi (π) és un nombre important utilitzat en diverses fórmules. Si utilitzeu una calculadora, premeu la tecla pi per obtenir resultats realment precisos. En cas contrari, per facilitar els càlculs, podeu arrodonir pi a uns quants dígits després de la coma, per exemple, 3, 14159. Si multipliqueu aquest nombre pel quadrat del radi, el resultat serà 615, 75164.

Pas 4. Divideix la mesura de l’angle per 360
Divideix l'angle del ventilador del sector per 360 (la mesura d'un angle de cercle complet). Per a l'exemple anterior, el resultat és al voltant de 0,166. Si el calculeu amb una calculadora, el resultat és realment més llarg i iteratiu, però aquí es redona per facilitar el càlcul.

Pas 5. Multiplicar aquest número pel número anterior
Multipliqueu el número que obtingueu després de dividir l'angle per 360, pel nombre que heu obtingut abans després de multiplicar pi pel quadrat del radi. per a l'exemple anterior, el resultat és 102, 214 (després de l'arrodoniment).
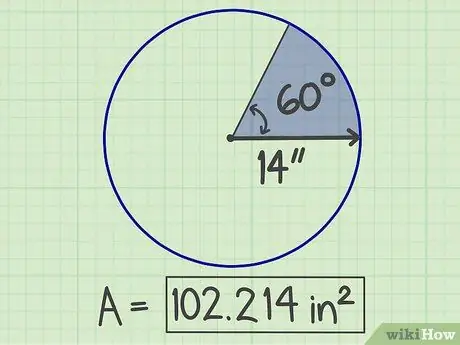
Pas 6. Escriviu els resultats
El nombre obtingut és la superfície del sector, que és de 102, 214 polzades quadrades.
Mètode 5 de 7: El·lipse
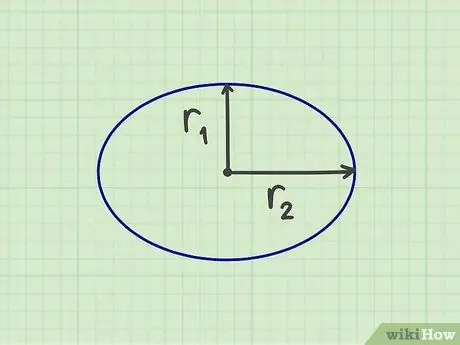
Pas 1. Mesureu el nombre requerit
Per calcular l'àrea d'una el·lipse, heu de mesurar dos "radis", és a dir, el radi curt i el radi llarg, que és la meitat de l'amplada i la meitat de l'alçada de l'el·lipse. També podeu mesurar el radi curt des del centre de l’el·lipse fins al costat més curt i el radi llarg des del centre de l’el·lipse fins al costat més llarg. El radi curt hauria de formar un angle recte amb el radi llarg.
Al món real, és possible que hàgiu de mesurar-lo vosaltres mateixos, però a l’hora de fer els deures, el professor normalment ja ha escrit els números juntament amb una imatge de la forma
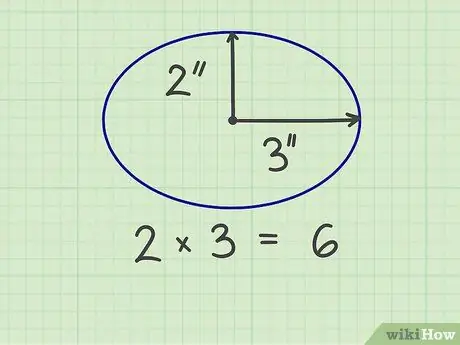
Pas 2. Multiplicar els dos dits
Per exemple, una el·lipse fa 6 polzades d'ample i 4 polzades d'alçada, de manera que els radis són de 3 polzades i 2 polzades. Quan es multipliquen els dos nombres, el resultat és 6 (3 x 2).

Pas 3. Multiplicar el resultat per pi
Pi (π) és un nombre important utilitzat en diverses fórmules. Si utilitzeu una calculadora, premeu la tecla pi per obtenir resultats realment precisos. En cas contrari, per facilitar els càlculs, podeu arrodonir pi a uns quants dígits després de la coma, per exemple, 3, 14159. Quan multipliqueu aquest nombre pel quadrat del radi, el resultat és 18, 84954.
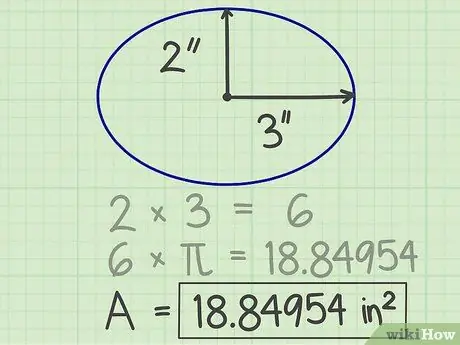
Pas 4. Escriviu els resultats
El nombre obtingut a partir del càlcul anterior és l’àrea de l’el·lipse. A l’exemple anterior, l’àrea de l’el·lipse és de 18,84954 polzades quadrades.
Mètode 6 de 7: Triangle
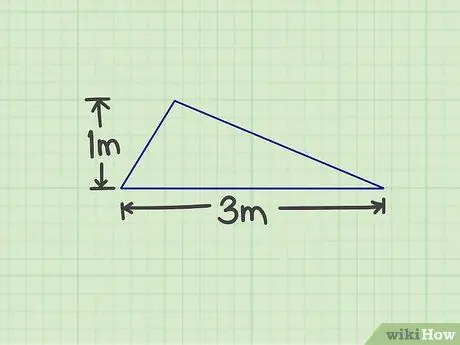
Pas 1. Mesureu el nombre requerit
Cal mesurar la base i l’alçada del triangle. Qualsevol costat del triangle pot ser la base, sempre que es pugui mesurar l’alçada. Per exemple, hi ha un triangle amb una base de 3 mi una alçada d’1 m.
Al món real, és possible que hàgiu de mesurar-lo vosaltres mateixos, però a l’hora de fer els deures, el professor normalment ja ha escrit els números juntament amb una imatge de la forma
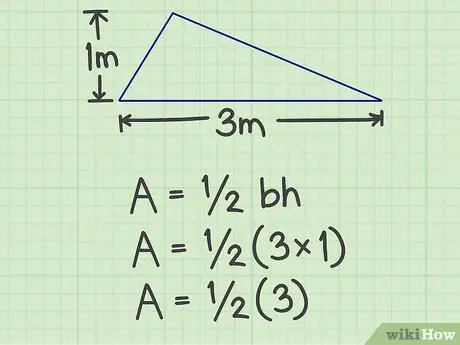
Pas 2. Multipliqueu la base per l'alçada
Per a l'exemple anterior, el resultat és 3 (3x1).
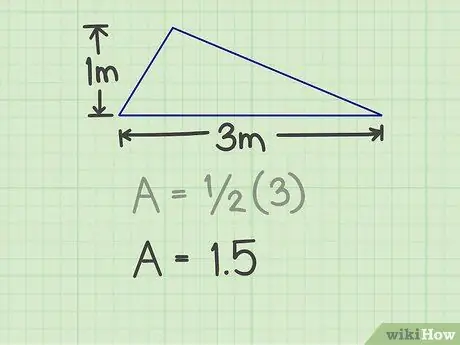
Pas 3. Multiplicar el resultat per 1/2
Aquesta multiplicació produirà els números 1, 5.
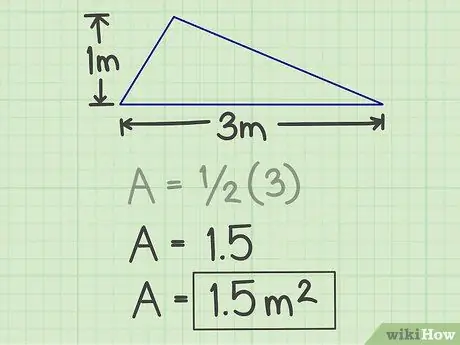
Pas 4. Escriviu els resultats
El nombre generat pel càlcul anterior és l'àrea del triangle i, amb l'exemple anterior, la seva àrea és d'1,5 metres quadrats.
Mètode 7 de 7: construcció plana complexa
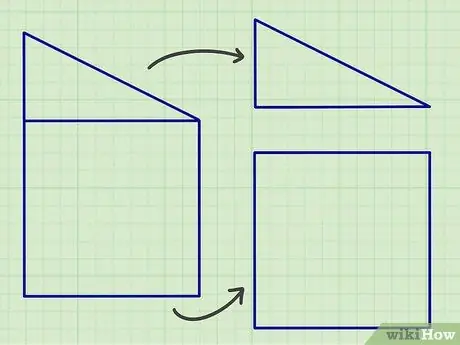
Pas 1. Separeu formes planes complexes en parts que consisteixen en les formes geomètriques estàndard anteriors
Si el que esteu fent és deures, pot ser fàcil dividir la forma complexa en les formes planes comentades anteriorment, però al món real, és possible que hagueu de dividir la forma plana en moltes formes planes per obtenir un resultat de càlcul precís..
Una bona manera de començar és buscar línies paral·leles o que formin un angle determinat, ja que la majoria de formes planes estan formades per aquestes formes
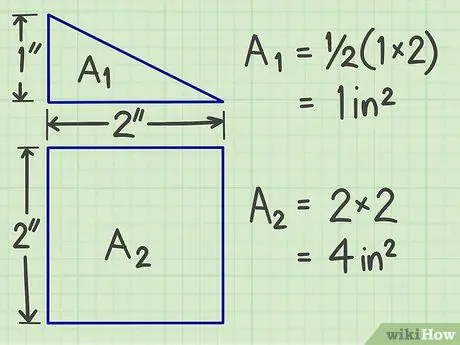
Pas 2. Calculeu l'àrea de cadascuna de les figures planes resultants de la separació
Utilitzeu els mètodes anteriors per obtenir l'àrea de cada forma plana.
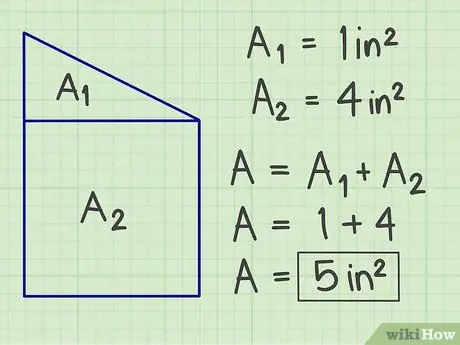
Pas 3. Sumeu els resultats
Sumeu totes les àrees calculades per obtenir l’àrea total de la vostra figura plana complexa.
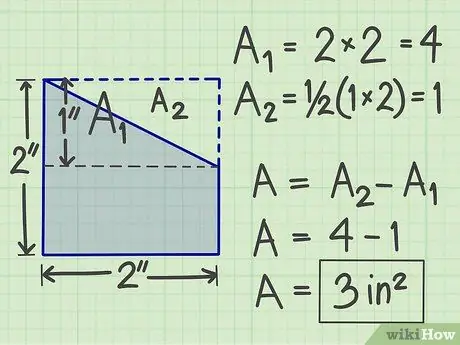
Pas 4. Utilitzeu un altre mètode
Hi ha moltes altres maneres de provar, en funció de la forma de la forma plana complexa. Per exemple, també podeu afegir-hi una forma de pla imaginari perquè es converteixi en una forma de pla geomètric estàndard. Després, calculeu l'àrea i resteu l'àrea de la forma plana imaginària que solíeu afegir.
Consells
- Utilitzeu aquesta calculadora si necessiteu ajuda per resoldre càlculs matemàtics.
- Demaneu ajuda a un amic si encara teniu problemes.
Advertiment
- Sempre és millor comprovar de nou els resultats del càlcul per assegurar-vos que siguin correctes.
- Assegureu-vos que les unitats que utilitzeu siguin iguals (cm, m, polzada, etc.) a l'hora de calcular, de manera que no obtingueu un mal càlcul a causa de les unitats mixtes.






